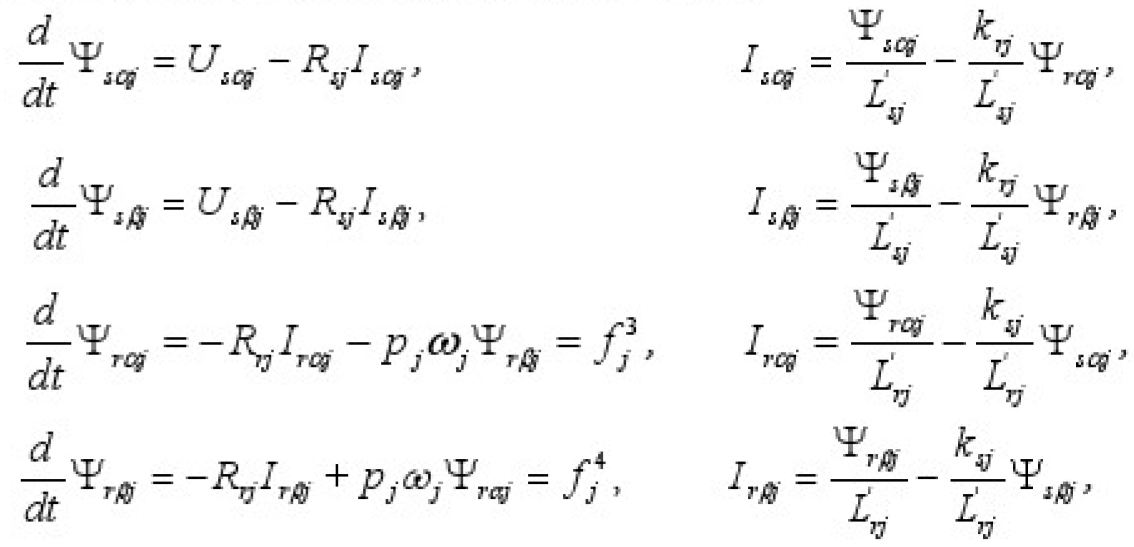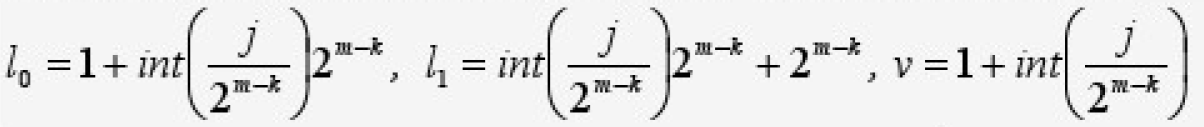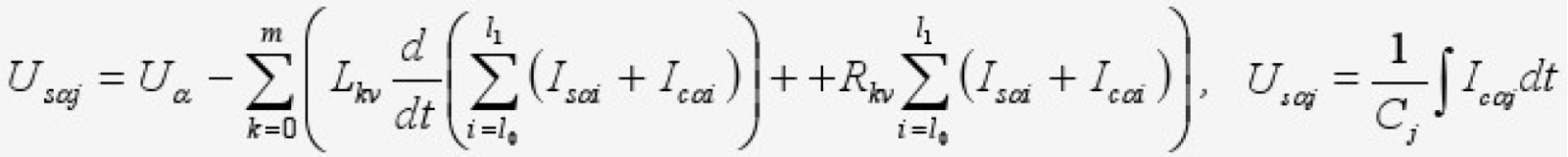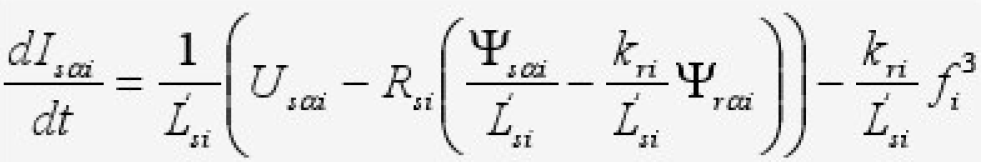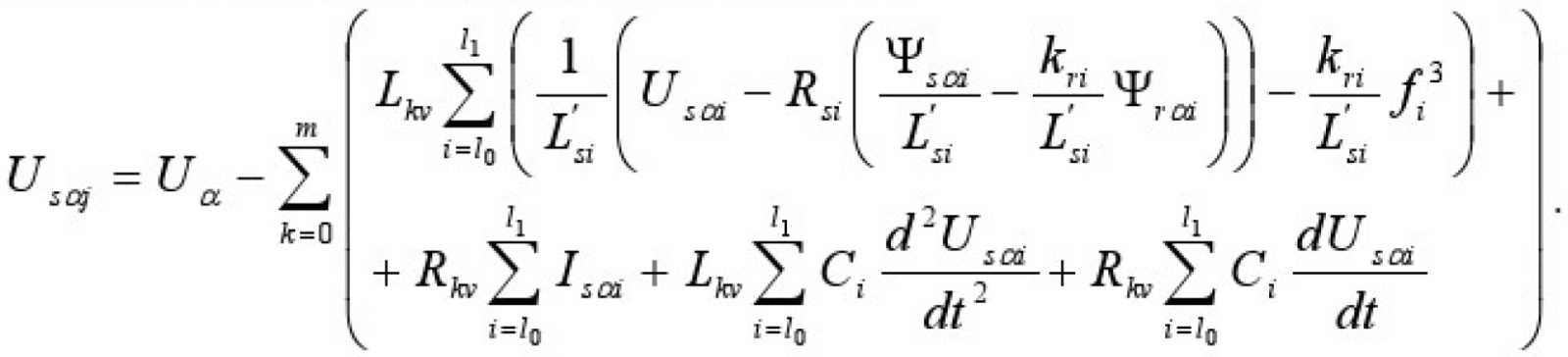Содержание
Проблема компенсации реактивной мощности (КРМ) остается одной из важнейших при эксплуатации систем электроснабжения (СЭС) с электродвигательной нагрузкой в виде асинхронных электродвигателей (АД) из-за продолжающегося роста мощностей используемых в приводах АД и цен на электроэнергию [1,2].
Ясно, что она напрямую связана с проблемой энергосбережения, так как около 60% всей реактивной мощности, связанной с образованием переменных магнитных полей, потребляют АД.
Проблематика КРМ и СЭС
Особого внимания заслуживает проблема КРМ в СЭС, где существенно влияние изменения состояния одного электродвигателя на состояние остальных как показано на рисунке 1:
В этой связи представляет интерес разработка расчетных процедур оценки необходимых величин компенсирующих емкостей в варианте индивидуальной КРМ АД, находящихся в общей системе электроснабжения.
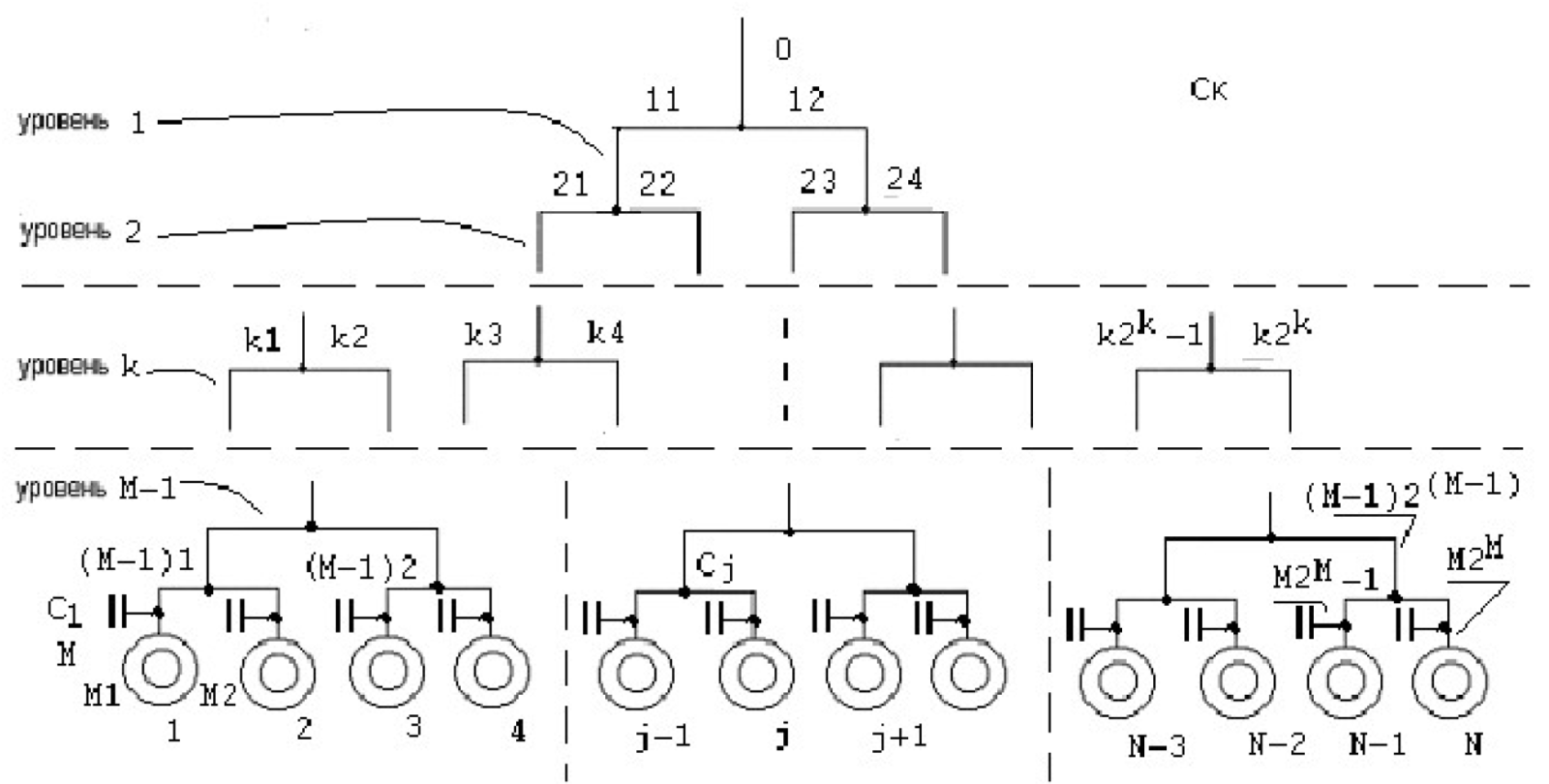
В работе [3] рассмотрено моделирование процессов электромеханического преобразования энергии в СЭС произвольной структуры рисунок 2:
где
- Индекс 0 — соответствует общему участку питающего кабеля.
- Для остальных кабелей первый индекс означает принадлежность уровню, второй — ветви соответствующего уровня.
- Диапазон изменения значений уровней kϵ (1,М), диапазон изменения индексов ветвей vϵ (1,2k).
При помощи такой системы индексации будем идентифицировать конкретные кабельные участки (ветви) системы электроснабжения.
Например, Lkv, Rkv— индуктивность и активное сопротивление кабельного участка k-го уровня, v-ой ветви, являющиеся функциями его длины.
В работе [3] получена математическая модель асинхронного электродвигателя, работающего в этой сети без учета возможных емкостей, присоединенных к статорам электродвигателей.
Состояние каждого j -го двигателя, работающего в одиночном варианте, обычно [4] описывается совокупностью дифференциальных и алгебраических связей (1):
где
- Параметры, начинающиеся с R и индексами s, r — активные сопротивления обмоток статоров и роторов АД.
- pj — число пар полюсов.
- ωj— геометрическая угловая скорость вращения ротора электродвигателя.
- Ψs, Ψr и Is, Ir с индексами α, β — составляющие потокосцеплений и токов статора и ротора по осям неподвижной системы координат.
- k, L — с индексами sj, rj коэффициенты электромагнитной связи и переходные индуктивности двигателей.
- j — в индексном обозначении определяет номер двигателя.
Ясно, что состояние каждого j-го электродвигателя по рисунку 2 определяется скоростью вращения ротора ωj и составляющими Usαj, Usβj по (1) напряжений статоров двигателей.
В этой связи рассмотрим алгоритм формирования упомянутых напряжений в системе электроснабжения по рисунку 2 с целью синтеза математической модели j-ro асинхронного электродвигателя.
Вывод прогрессивной математической модели для расчета систем электроснабжения с КРМ
В отличие от [3] будем производить учет компенсирующих емкостей – Cj, jϵ (1,N) на рисунке 2, тогда получим следующее уравнение:
Основная идея при определении напряжений на обмотках статора j-ro электродвигателя заключается в следующем:
- Идентификация путей от двигателей до источника питания и идентификация диапазонов номеров двигателей, токи которых участвуют в формировании суммарных падений напряжений на каждом кабельном отрезке — ветви при помощи аналитических конструкций (2).
- Где l0, I1 — начальное и конечное значения индекса, определяющего номер двигателя, токи которого участвуют в формировании падения напряжения на k, v -участке кабельной сети.
С учетом последнего, искомое напряжение на обмотке статора j-го электродвигателя (для составляющей по координатной оси α)1:
Здесь Icαi емкостная составляющая тока статора. Учитывая, что последнее выражение можно переписать следующим образом:
где
- Cj— компенсирующая емкость фазы обмотки статора i-го АД.
Из уравнения (1) следуют следующие зависимости:
Поэтому для составляющей напряжения статора АД получаем выражение:
Дальнейшие преобразования дают следующее выражение:
Обозначаем следующую зависимость:

В итоге получим совокупность алгебраических и дифференциальных связей, описывающих состояние j- го асинхронного электродвигателя с короткозамкнутым ротором в общей системе электроснабжения:
где
- jϵ(1,N).
Для использования в расчетной практике получили математические модели электромеханического преобразования энергии с возможностью КРМ совокупностью N асинхронных электродвигателей с короткозамкнутым ротором, находящихся в системе электроснабжения произвольной структуры.
На основании данной модели разработано соответствующее программное обеспечение, которое позволяет задавать конфигурацию системы электроснабжения, а именно:
- Длины и параметры ветвей кабелей.
- Количество электродвигателей.
- Параметры электродвигателей.
- Последовательности включения или отключения электродвигателей для имитации реальных процессов пусков и отключений приводов машин.
- Определение характера нагрузки на электродвигателях при моделировании режимов работы реальных машин и величины емкостей устройств КРМ.
Расчет примера системы на основании полученной математической модели
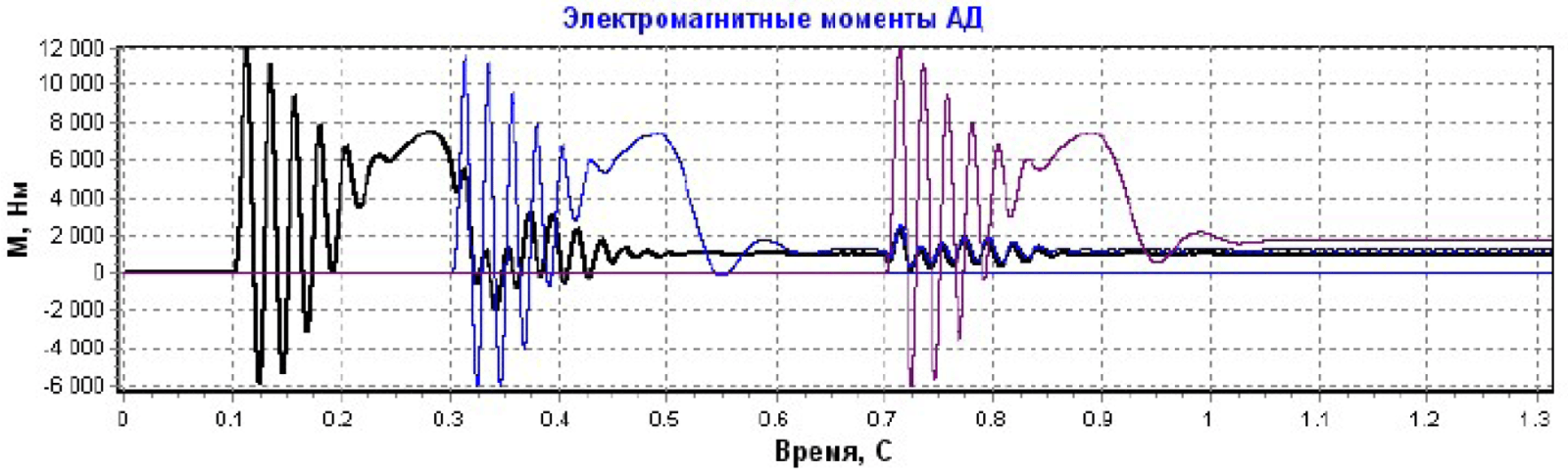
На рисунке 1 приведены результаты расчетных осциллограмм изменений электромагнитных моментов при последовательном пуске трех асинхронных электродвигателей ABP280L4 номинальной мощностью 160 кВт, подключенных к источнику питания в соответствии с рисунком З:
При расчетах применялись следующие условия:
- Временные интервалы включения двигателей уменьшены с целью иллюстрации влияния изменений в режиме работы каждого из них на состояние остальных.
- Включение КРМ происходило через 1.6С после пуска первого АД.
- Величины компенсирующих емкостей принимались одинаковыми — 72.2 мкФ.
- Значения косинусов ϕ вычислялись как значения косинусов углов между мгновенными значениями векторов напряжений и токов электродвигателей.
Пуски производились до уровней установившихся значений моментов сопротивлений на валах электродвигателей соответственно:
- Mc1 =1000 Нм.
- Мc2 = 1250 Нм.
- Mc3=1500 Нм.
Характер изменения величин косинусов ϕ при пусках АД и включении КРМ при одинаковых величинах емкостей (72.2 мкФ) при обеспечении одинаковых значений cos(ϕ)=0.833 АД представлены на рисунках 4 и 5:
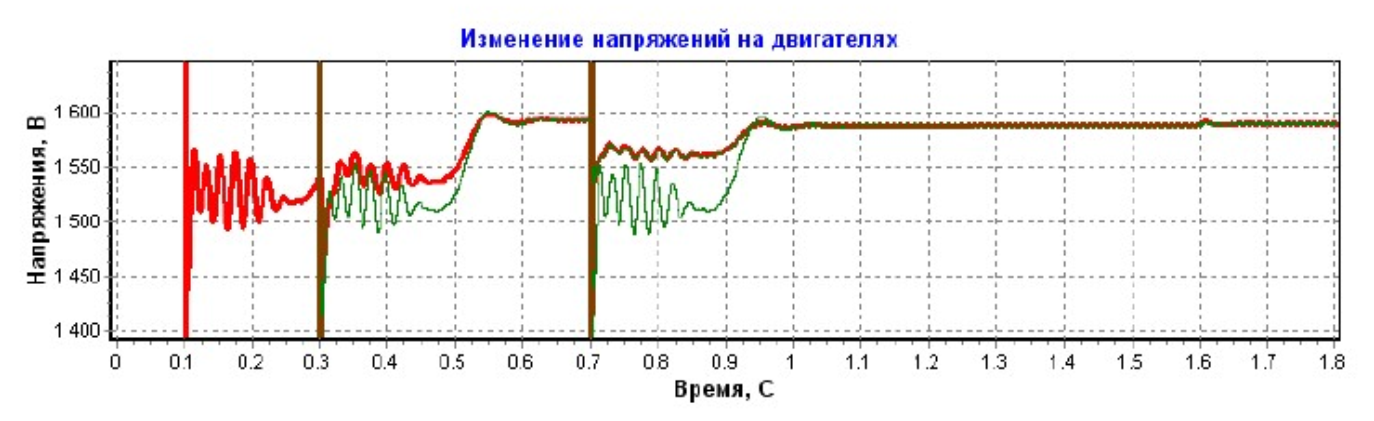
Характер изменения напряжений на АД и падения напряжений в кабельных сетях от источника питания до электродвигателей представлены на рисунках 6 и 7:
В результате применения КРМ произошло следующее:
- Величина тока в общем участке кабельной сети уменьшилась (амплитудные значения) с 420А до 318А.
- Потребляемая мощность из сети при этом уменьшилась с 680 кВт до 510 кВт.
- При обеспечении всем АД номинального для этик двигателей значения cos(ϕ)=0.833 потребляемая мощность из сети уменьшилась с 680 кВт до 430 кВт.
При значениях компенсирующих емкостей соответственно для следующих электродвигателей:
- M1 — С1=129 мкФ.
- М2 — С2=110,6 мкФ.
- М3- C3=76.8 мкФ.
На основе предложенной математической модели возможно получение необходимой информации о состоянии электромеханических систем при преобразовании электрической энергии в системе электроснабжения произвольной структуры с электродвигательной нагрузкой в виде:
- Трендов основных характеристик электродвигателей.
- Трендов основных характеристик с применение КРМ.
Список литературы
- Компенсация реактивной мощности, к вопросу о технико-экономической целесообразности / Овсейчук Г. // Новости электротехники: информационно — справочное издание — 2008 -№4(52).
- Tractive Power Compensation Technologies, State — of — the Art Preview / Dixon J.
- Ещин Е.К. Модель асинхронного электродвигателя в системе электроснабжения // Электротехника-2002. -№1. С.40-43
- Ковач К., Рац И. Переходные процессы в машинах переменного тока. -М. -Л.: Госэнергоиздат, 1963 -744 с.
- Модель типового модуля системы электроснабжения с коммутационной аппаратурой.
- Модель магистральной структуры электроснабжения для исследования режимов работы совокупности асинхронных двигателей.
- Моделирование перенапряжений в системе электроснабжения с электродвигательной нагрузкой.
Источник: Моделирование процессов компенсации реактивной мощности в системе электроснабжения с электродвигательной нагрузкой / Е.К. Ещин // Вестник КузГТУ. — 2012. — №2. — C. 48-52.