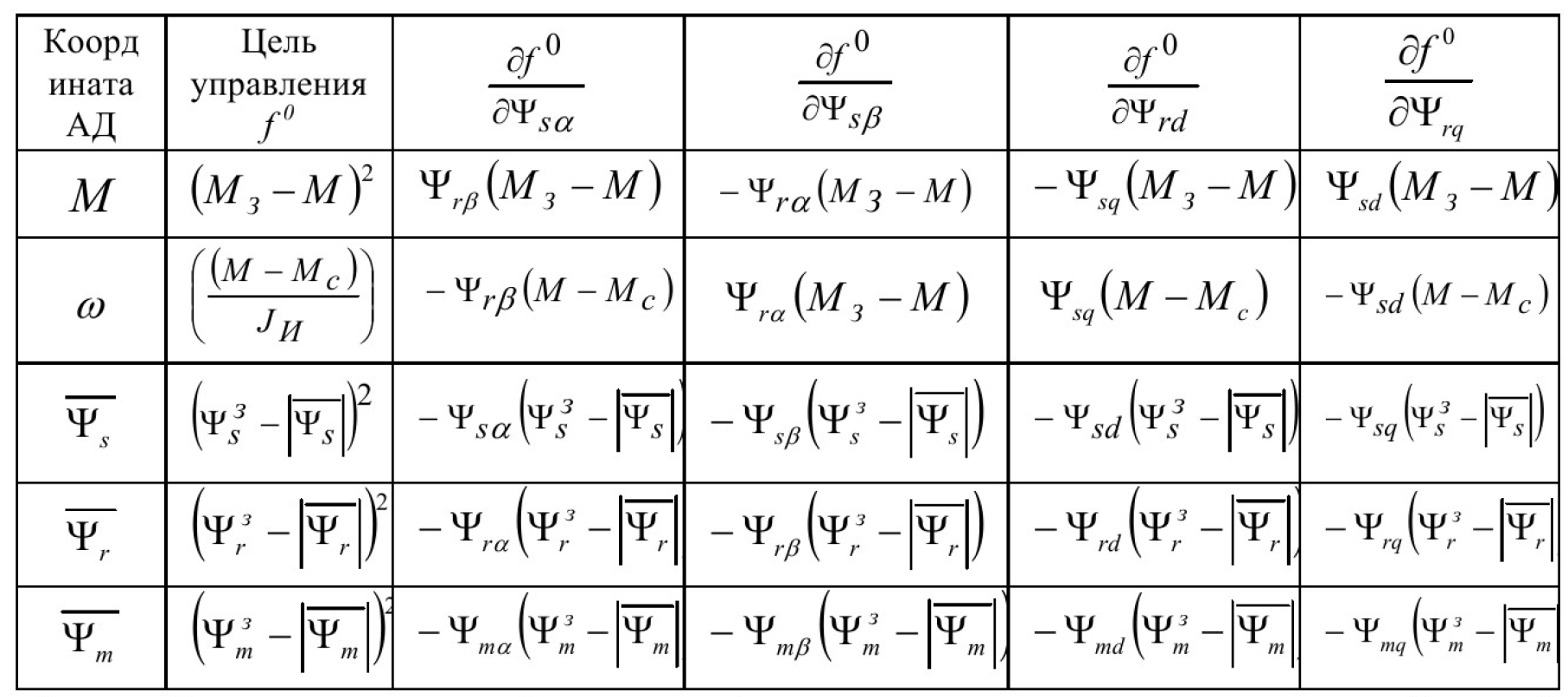Известно множество вариантов управления координатами асинхронного электродвигателя (АД). Но лишь некоторые из этих вариантов нашли широкое применение и, по сути, являются стандартами современного электропривода [1, 2].
Существуют следующие методы управления электроприводом:
- Скалярное частотное управление, предложенное М.П. Костенко в 1925 г.
- Поле-ориентированное управление (FOC — Field Oriented Control), впервые представленное Ф. Блашке (F. Blaschke) в 1971 г.
- Прямое управление моментом (DTC — Direct Torque Control), полученное М. Депенброком (М. Depenbrock) в 1985 г. [3] и независимо И. Такахаши и Т. Ногучи (I. Takahashi, T. Noguchi) в 1986 г.
Неоспоримым достоинством первого варианта является его простота, поэтому он вполне удовлетворяет требованиям электроприводов с медленно изменяющейся нагрузкой и небольшим диапазоном регулирования. Но для электропривода, где требуются хорошие динамические показатели, он неприменим. В этом случае целесообразно использовать один из вариантов векторного управления. Недостатком векторных вариантов управления является чувствительность к изменению параметров АД (в особенности активных сопротивлений обмоток статора и ротора). Менее чувствительным к изменению параметров является вариант — прямое управление моментом (DTC). Кроме того, он обеспечивает наискорейшее регулирование электромагнитного момента и потока статора АД.
Существует также множество работ, посвященных применению теории оптимального управления к решению задачи управления координатами АД [4, 5]. Достоинством предложенных конструкций управляющих устройств является их универсальность с точки зрения выбора цели управления (будь то регулирование электромагнитного момента или потокосцеплений).
В связи с этим сформулируем задачу управления переменными АД как задачу минимизации некоторого функционала, записанного в интегральной форме и выражающего цель управления в общем виде:

Состояние АД будем описывать системой дифференциальных связей (1), определяющих характер изменения фазовых координат (составляющих векторов потокосцеплений статора (Ψsu, Ψsv) и ротора (Ψru , Ψry ) по осям синхронной системы координат u-v) с выделением в них управляющих воздействий — составляющих напряжений статора и ротора по осям координатной системы — Usu, Usv, Uru, Urv :

(1)
где
- ω — круговая частота вращения ротора двигателя
- Rs, Rr, Ls‘, Lr‘, ks, kr — активные сопротивления статора, ротора, переходные индуктивности статора и ротора, коэффициенты электромагнитной связи статора и ротора соответственно.
Возмущающим воздействием будем считать круговую частоту вращения ротора ω. Это допустимо, если цель управления будет связана исключительно с состоянием только двигателя.
Условие введения управления со стороны статора (ротора) требует или наличия в подынтегральной функции f° информации о состоянии статора (ротора), или присутствия управлений, или того и другого вместе. В противном случае следует ожидать аналитической неразрешимости задачи. Решение можно получить, используя принцип максимума Л. Понтрягина [6].
При этом требуется образование вспомогательной функции:

где
Ψi — компоненты вспомогательной вектор — функции Ψ.
Условие абсолютного экстремума для задач, линейных относительно управляющих воздействий может быть записано в виде:

Если управление двигателем производится со стороны статора, то условия оптимальности процесса управления после нахождения аналитических конструкций и координатных преобразований для Ψi будут выглядеть следующим образом.
В неподвижной системе координат α-β:

(2)
где
- Us max — максимально возможное значение составляющей вектора напряжения статора
В системе координат d-q, неподвижной относительно ротора:

(3)
Если управление производится со стороны ротора, то условия оптимальности процесса управления.
В системе координат α-β:

(4)
где
- Ur max — максимально возможное значение составляющей вектора напряжения ротора
В системе координат d-q:

(5)
При одновременном управлении со стороны статора и со стороны ротора (машина двойного питания) должны выполняться условия оптимального управления со стороны статора (2), (3) и со стороны ротора (4), (5).
В качестве примера рассмотрим задачу управления величиной электромагнитного момента АД. В этом случае целевой функционал будет:

где
- М3, М — задаваемое и мгновенное значение электромагнитного момента АД соответственно
- to, ti — время начала и завершения процесса управления.
Если f0= (M3 — M)2, то условия (2), (3), (4) и (5) будут выглядеть.
В системе координат α-β:

В системе координат d-q:

Результаты компьютерного моделирования электромеханических процессов АД ВРП160М4 при управлении электромагнитным моментом показаны на рис. 1 и рис. 2, где до 0,3 с на вал двигателя действует реактивный момент сопротивления Мс, который затем приобретает пульсирующий характер, а в 0,54 с начинается управление электромагнитным моментом АД с целью его стабилизации на уровне 100 Нм. Заданная цель достигается за время меньшее 0,001 с, и при этом формируется годограф потокосцепления статора (показан на рис. 2) в форме шестиугольника, что имеет место при классическом DTC.
Некоторые примеры использования алгоритма для получения аналитических конструкций устройств управления координатами АД приведены в табл. 1, где Ψs2, |Ψ̅s|, Ψr2, |Ψ̅r|, Ψm2, |Ψ̅m| — задаваемые и действительные значения амплитуд векторов потокосцеплении статора, ротора и главного магнитного потока соответственно.
Таким образом, предложенный алгоритм формирования аналитических конструкций устройств управления состоянием асинхронных электродвигателей позволяет получать физически реализуемые устройства управления минимальной сложности при различной целевой формулировке задач управления.
Список литературы
- Bocker Joachim, Mathapati Shashidhar. State of the art of induction motor control / Electric Machines & Drives Conference, 2007. IEMDC ’07. IEEE International, Publication Date: 3-5 May 2007 Volume: 2, on page(s): 1459-1464.
- Tripathi A., Anbarasu R.S., Somakumar R. Control of AC Motor Drives: Performance Evaluation of Industrial State of Art and New Technique / Industrial Technology, 2006. ICIT 2006. IEEE International Conference on Publication Date: 15-17 Dec. 2006. On page(s): 3049-3054.
- Depenbrock Manfred. Direct self-control of the flux and rotary moment of a rotary field machine: United States Patent, № 4,678,248, jul. 7, 1987. — sheets 4.
- B. Садовой, A.A. Дерец, Ю.Ю. Шрамко. Релейная система векторного управления следящим электроприводом на базе машины двойного питания // Электротехника. М., 1999, №5. С. 47-51.
- Гаврилов П.Д., Ещин Е.К. Общая задача оптимизации частотного управления асинхронным электродвигателем //Изв. вузов. Электромеханика.- 1979. №6. С.541-545.
- Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов .-4-е изд. -М.: Наука, 1983. -392 с.
Источник: Оптимальное управление координатами асинхронного электродвигателя / А.В. Григорьев // Вестник КузГТУ. — 2008. — №6. — C. 29-32