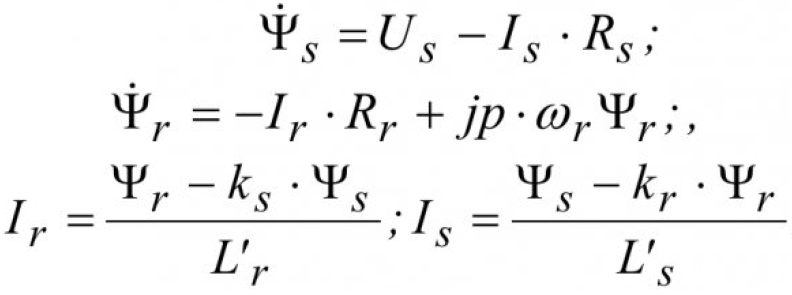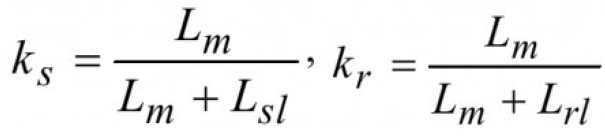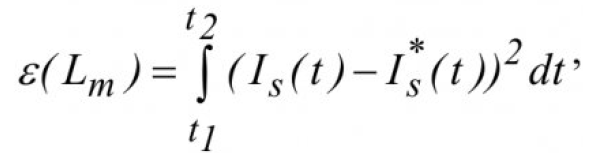Содержание
Как показано в работе [1], при оценке параметров и состояния асинхронного электродвигателя с короткозамкнутым ротором (АД) величина индуктивности цепи намагничивания мало влияет на точность оценок, при условии ее достаточно большого по сравнению с индуктивностями рассеяния значения.
Вывод расчетных уравнений для оценки индуктивности
Данное суждение справедливо для переходных процессов, например процесса для следующих режимов:
- Пуск электродвигателя, когда величины намагничивающего тока и потокосцепления цепи намагничивания относительно малы.
- При статических режимов работы электродвигателей с существенным скольжением.
Чем ближе режим работы машины к режиму холостого хода, тем сильнее сказывается влияние индуктивности цепи намагничивания Lm на точность оценок состояния асинхронного электродвигателя, но, с другой стороны, более точно можно оценить саму величину Lm.
Для оценки индуктивности цепи намагничивания воспользуемся следующей моделью для электродвигателя:
где
- Ir — вектор тока ротора.
- Is — векторы силы тока статора.
- Us — векторы напряжения статора.
- Rr — активные сопротивления ротора.
- LrI — индуктивности рассеяния ротора.
- Rs — активные сопротивления статора.
- Ψr — векторы потокосцепления ротора.
- Ψs — векторы потокосцепления статора.
- LsI — индуктивности рассеяния статора.
- р — число пар полюсов электродвигателя.
- Lm— индуктивность цепи намагничивания.
- ωr — частота вращения ротора электродвигателя.
Следовательно коэффициенты электромагнитной связи статора и ротора определим из следующих уравнений:
Поэтому переходные индуктивности статора и ротора определяем следующим образом:
Есть ряд параметров и величин определяющие состояние электродвигателя определяются согласно следующих работ [1, 2], при этом знание величины индуктивности цепи намагничивания не требуется.
К данным параметрам относятся следующие параметры электродвигателя: величин:
- L’r — индуктивность ротора.
- L’s — индуктивность статора.
- Rr — активные сопротивления ротора.
- Ψr — векторы потокосцепления ротора.
- Rs — активные сопротивления статора.
- Ψs — векторы потокосцепления статора.
- ωr — частота вращения ротора электродвигателя.
Определение величины Lm будем производить следующим образом:
- Берем относительно небольшую выборку по времени порядка 20-60 мс, то есть 1-3 периода сетевого напряжения.
- Выполняем минимизацию квадратичной ошибки с помощью интегральной зависимости.
Тогда минимизация квадратичной ошибки примет вид:
где
- Is (t) — расчётные величины тока статора.
- I*s (t) — измеренные величины тока статора.
Расчет производим методом Эйлера согласно уравнения (1), а начальное значение получаем по формуле:
Практические расчеты и выводы
Поскольку варьируемый параметр только один, то численная минимизация целевой функции ε (Lm) не вызывает трудностей и может быть реализована любым из известных методов.
Проверка метода была проведена на математической модели, а также практически по результатам пуска нескольких электродвигателей.
Результаты оценок для электродвигателя 4АМ80А4 мощностью 1.1 кВт приведены на рисунке 1:
На графике изображена измеренная скорость вращения и результаты оценок с различными размерами выборки периода сетевого напряжения:
- 2.
- 2,2.
- 2,4.
- 3.
Найденная из опыта холостого хода индуктивность цепи намагничивания для этого асинхронного электродвигателя составила 0,243 Гн.
По графикам хорошо видно, что погрешность оценок максимальна в переходном процессе, где:
- Погрешность достигает 15%, и чем ближе режим работы к режиму холостого хода, тем меньше погрешность.
- В свою очередь в установившемся режиме погрешность не превышает 5%.
Данная работа является продолжением работы [1] и полученные результаты доказывают возможность осуществления динамической идентификации асинхронных электродвигателей на основе предложенного варианта математической модели АД с упрощениями, основанными на учете значимости ее параметров в различных режимах.
Основным достоинством изложенного метода идентификации электродвигателя является возможность определения текущих значений параметров непосредственно в процессе функционирования асинхронного электропривода, а также устойчивость вычислительных процедур процесса идентификации.
Полученная таким образом информация может быть использована:
- Для функционального диагностирования АД.
- Для превентивной защиты электродвигателя.
- Для управления асинхронными электроприводами.
Список литературы
- Динамическая идентификация асинхронных электродвигателей с учетом значимости параметров.
- Каширских В.Г., Нестеровский А.В., Оценка активного сопротивления ротора асинхронного электродвигателя с помощью искусственной нейронной сети// Вести КузГТУ, 2004 год, №6, страницы 64-65.
- Обзор типов искусственных нейронных сетей и методов их обучения.
Источник: Оценка индуктивности цепи намагничивания асинхронного электродвигателя в процессе его работы / В.Г. Каширских, А.В. Нестеровский // Вестник КузГТУ, 2005 год, №2, страницы 28-29.