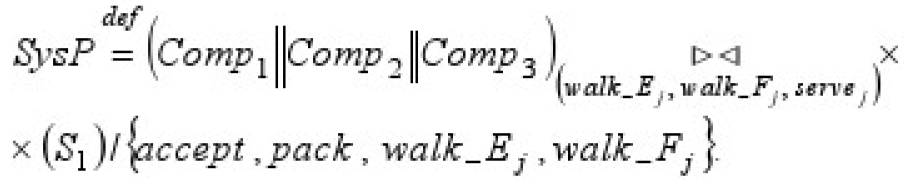Содержание
В работе рассмотрено исследование моделирования оценки характеристик с использованием языка РЕРА.
Полученные примеры при исследовании моделирования будут использоваться, чтобы показать методы упрощения модели.
При исследовании рассматриваются и сравниваются различные системы:
- Асимметричные.
- Симметричные системы MSMQ со случайным опросом.
Они являются расширением традиционной системы опроса и обычно применяются к моделям, в которых множественные ресурсы разделены среди нескольких пользователей, возможно с различными требованиями согласно, исследований [1-14].
Приведённые примеры включают локальные сети с многочисленными маркерами и сетями взаимосвязи мультишин в распределенных системах. Подобные системы были исследованы в работах [15-29].
Далее приводится подробная информация о каждой модели, указываются значения применённых параметров, и приводятся графики, показывающие изменение среднего времени ожидания в зависимости от изменения условий в данной системе.
Асимметричная система MSMQ со случайным опросом
Рассмотрим асимметричную систему, в которой ёмкости узлов в системе отличаются.
В системе имеются три узла:
- Два с ёмкостью 1.
- Один с ёмкостью 2.
Случайный опрос в системе означает, что при переходе от узла сервер может перейти к любому узлу, даже к тому же самому узлу снова.
Обслуживание ограничено, так как сервер, достигающий узла Node1, когда он полон, мог бы перед переходом обслужить только одного представителя клиента.
Однако, если второй сервер прибывает позже, в то время как первое обслуживание все еще происходит, то он может одновременно занять узел.
Система может быть классифицирована как:

Обгон разрешен в том смысле, что сервер при достижении узла не находит клиента и будет переходить дальше.
Модель этой системы на языке РЕРА приведена на рисунке 1:
Предполагаем, что Node1 это узел с характеристиками, которые отличают не только его большую ёмкость, но также и более скоростной ответ на вопросы сервера.
Теперь эти вопросы представлены раздельно при проходе (pass) действий или при включении (engage).
Предполагаем, что найдется процесс, производящий места для каждого клиента в буфере для узла так, чтобы оценка прибытия, когда буфер пуст, была удвоенной оценкой прибытия, в случае, когда одно место в буфере уже занято.
В компоненте сервера S действие блуждания (walk) представлено тремя различными действиями, каждое с оценкой деятельности ω/3, вероятность каждого из результатов есть 1/3.
Sj обозначает представитель сервера в узле Nodej, когда его можно включать (engage) или проходить (pass) в зависимости от того, есть ли требования у клиента по обслуживанию узла или нет.
На рисунке 2 показана модифицированная версия узла Node2:
В этой второй версии предполагаем, что есть дефект в Node1 такой, что не можем гарантировать, правильно ли ответит сервер, когда буфер полностью пуст или полностью полон:
- В случае, когда только одно место в буфере занято, то с вероятностью 0.5 он ответит, что как будто буфер был пуст.
- В случае, когда один клиент уже находится в обслуживании, но другое место в буфере также занято, он так же потерпит неудачу с вероятностью 0.5, разрешая второму серверу уйти без обеспечения обслуживания.
Исследуем влияние этого дефекта на среднее время ожидания клиента в этом узле и в других узлах. Во всех узлах, когда сервер занят, оценка того, какое обслуживание происходит, определяется сервером.
В системе нет никакой кооперации ни между этими тремя узлами, ни между двумя серверами.
Однако, действия passj, engagej и подача (serve) происходят при кооперации между узлом и сервером. Значения, которые были заданы для параметров, указаны в таблице 1:
Модель системы, свободная от дефектов, имеет:
- 368 состояний.
- 1570 переходов.
Модель дефектной системы имеет:
- 1618 состояний.
- То же самое число переходов 1570.
Среднее время ожидания в каждом узле было вычислено с использованием закона о малом числе испытаний, в то время как для каждой из моделей среднее время блуждания было различно.
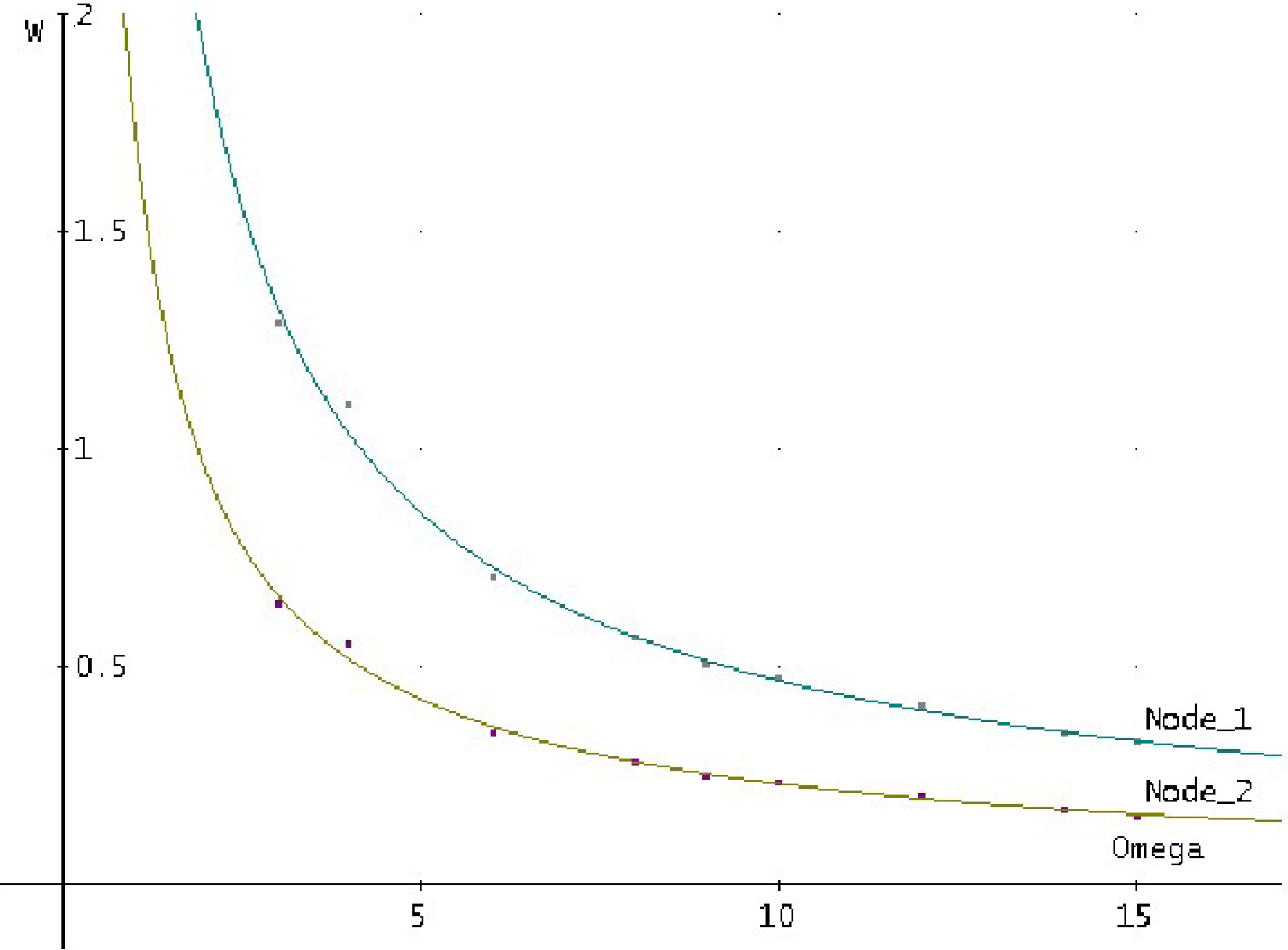
Результаты, показанные на рисунках 3 и 4, были сравнены, для того чтобы оценить эффект дефектного соединения Узлы Node2 и Node3 имеют те же особенности, что только для узла Node2 указаны на графиках.
Зависимость время ожидания Клиента в стабильной системе, представлена на рисунке 3:
Математическая модель зависимости времени ожидания W клиента в системе без дефекта от оценки блуждания ω, представленная на рисунке 3, будет иметь следующие виды.
Для узла Node_1:

Для узла Node_2:

Зависимость время ожидания Клиента в сбоящей системе, представлена на рисунке 4:
Математическая модель зависимости времени ожидания клиента W в дефектной системе от оценки блуждания ω, представленная на рис. 4, будет иметь следующие виды для узлов.
Для узла Node_1:

Для узла Node_2:

В системе, свободной от дефекта, MSMQff можно увидеть:
- Что хотя предполагаемое время ожидания одинаково во всех узлах, клиенты в узле Node1 испытывают несколько более длинные задержки.
- Для всех узлов уменьшено среднее время ожидания, когда уменьшено ожидаемое среднее текущее время серверов.
В случае дефектной системы MSMQwf можно увидеть:
- Что предполагаемое время ожидания клиентов в узле Node2 или Node3 при дефекте совсем не изменяется.
- Однако предполагаемое время ожидания клиентов в узле Node1 значительно увеличивается, особенно, когда оценка деятельности блуждания является замедленной.
Симметричная система MSMQ со случайным опросом с детальными узлами
Последняя рассматриваемая модель показывает, что система MSMQ обычно вложена в большую систему, и демонстрирует, как легко это смоделировать в модели на языке РЕРА.
В работе [21] автор выдвигает на первый план вложение модели опроса в глобальную модель.
Рассмотрена симметричная система MSMQ с ёмкостью узла 1 и ограниченным обслуживанием, в которой разрешен обгон.
Это можно классифицировать как систему:
- М/М/М/1/Qx1/L.
Подобную систему, асимметричной модели, представленной в предыдущем разделе статьи, в случае m=1.
Однако теперь также считается, что компоненты системы ответственны за генерирование клиентов, которые достигают узлов.
В данном случае предполагается:
- Что каждый клиент, это фактически пакет и часть сообщения.
- Для того, чтобы передать каждое сообщение, может быть необходимо несколько пакетов.
Модель этой расширенной системы указана на рисунке 5:
Аспекты MSMQ системы подобны моделям, представленным в предыдущем разделе.
Однако отметим, что деятельность in теперь просто представляет поставку пакета с генератора на буфер.
Оценка этой деятельности определена генератором, работающим на основании следующих принципах:
- Предполагается, что процесс прибытия описывается законом Пуассона, с оценкой λ, поставляющей сообщения генератору о готовности их принять. Это представляется принимающей деятельностью (accept).
- Каждое принятое сообщение разбито на пакеты (pack). Предполагается, что средняя длина сообщения — М пакетов. Пакеты поставляются в буфер по одному, с помощью in деятельности.
- Когда закончилось обслуживание пакета, он будет заменен другим, пока все сообщение не будет отправлено. Тогда возобновляется процесс прибытия.
Так как среднее число пакетов в сообщении — М, когда обслуживание пакета закончено, другой пакет уже доступен с вероятностью М—1/М.
Таким образом, пассивная деятельность подачи (serve) с этим результатом имеет вес М—1, тогда новое сообщение с вероятностью 1/М должно быть обработано прежде, чем доступен другой пакет.
Итак, вес деятельности подачи, которая возобновляет процесс прибытия, равен 1.
Теперь узлы системы представлены:
- Сложными компонентами Compj.
- Кооперацией «генератора» Genj
- Кооперацией «узла», Node
Эти компоненты должны кооперировать действия in и servej, следовательно, они объединены друг с другом как серверы.
Действия блуждания требуют кооперации сервера и соответствующего соединения, речь идет о следующих функциях:
- walk_E
- walk_Fj.
- servej.
Это означает, что три компонента, Genj, Nodej и Sj должны кооперироваться так, чтобы была достигнута servej деятельность.
Модель имеет:
- 888 состояний.
- 3858 переходов.
Значения параметров указаны в таблице 2:
Поскольку система симметрична, особенности характеристики всех узлов одинаковы, поэтому:
- Вместо среднего времени ожидания клиента, или пакета, в узле вычисляют среднее время передачи сообщения.
- Используем закон о малом числе испытаний, который сейчас применен к сложной паре узлов.
- Находим среднее число сообщений (messages) в узле Nm, отмечая, что найдется один представитель сообщения всякий раз, когда не разрешена принимающая (accept) деятельность.
Поэтому полагаем полную деятельность равной 1, найдем Raccept и выводим, что:
- Nm=1-Raccept.
Находим пропускную способность сообщения, Хm, полагая вероятность деятельности (serve, w2,ꓕ) равной 1/Мхμ всякий раз, когда посланы все пакеты сообщения.
Предполагаемое время передачи сообщения в системе:
- Тm, тогда Тm=Nm/Хm.
Значение предполагаемого времени передачи, когда среднее число пакетов в сообщении М, изменяется в пределах от 5 до 30, рисунок 6:
Математическая модель зависимости времени передачи сообщения W от среднего числа пакетов в сообщении n, представленная на рисунке 6, будет иметь вид для следующих функций.
Для System:

Для SysP:

Это сравнение с предполагаемым временем передачи сообщений той же самой длины в родственной модели опроса SysP:
Основные выводы по изысканиям
Анализ результатов полученных на основе изучения асимметричной и симметричной систем (MSMQ) со случайным опросом показывает практические преимущества создания моделей по сравнению с простыми системами.
Использование асимметричных и симметричных систем (MSMQ) со случайным опросом базируется на способности строго бигомотетичных компонент выполнять действия, приводящие к производным множествам, поэтому:
- Эти производные множества в свою очередь сами строго бигомотетичны.
- Одним из методов упрощения модели могут быть отношения между строгим биподобием и основным марковским процессом.
- При упрощении модели находят компоненты, которые выполняют одинаковые действия.
- Для гарантии поведения компонент проверяют, действительно ли является тем же самым.
С точки зрения алгебры процесса, если для одной компоненты найдется меньшее производное множество, то она может заменить другую компоненту в модели и привести к пространству состояний основного марковского процесса.
Практическое применение данного подхода автоматического формирования модели с помощью асимметричных и симметричных систем (MSMQ) со случайным опросом заключается в динамическом планировании задач в параллельных и распределенных приложениях.
Подобные подходы важны в системах, где модель должна обновляться постоянно и динамически в зависимости от текущего состояния ресурсов.
Такой подход к формированию РЕРА-модели надёжности основан на применении асимметричных и симметричных систем (MSMQ) со случайным опросом для смоделированных компонент системы.
Так как строгое биподобие есть отношение соответствия для асимметричных и симметричных систем РЕРА, то оно наиболее полно удовлетворяет условиям отношения строгого бимоделирования.
Использование асимметричных и симметричных систем (MSMQ) со случайным опросом применено для упрощения пространства состояний одной из моделей.
Список литературы
- Сорокин А.С., Парадигмы программирования и алгебра процесса моделирования характеристик // Вестник КузГТУ, 2011 год, № 4 (86). Кемерово, С. 77-82.
- Сорокин А.С., Алгебра процесса моделирования характеристик //Вестник КузГТУ, 2011 год, №5 (87). Кемерово, С. 105-109.
- Сорокин А.С., Модели симметричных систем опроса в теории организации очередей // Вестник КузГТУ, 2011 год, №6 (88) Кемерово, С. 66-71.
- Моделирования характеристик систем мультисервер-мультиочереди MSMQ.
- Aldinucci М., Danelutto М., Algorithmic Skeletons Meeting Grids. // Parallel Computing, 32 (7-8). 2006, p 449-462.
- Hillston J., A Compositional Approach to Performance Modelling. Cambridge University Press, 1996.
- Сорокин A.C., Применение полумарковских процессов к определению характеристик надежности технологических схем //Вестник КузГТУ, 2005 год, №1 (45), Кемерово, С. 3-9.
- Сорокин А.С., Структурное моделирование надежности технологических систем с использованием скелетонов// Вестник КузГТУ, 2008 год, №4 (68), Кемерово, С. 31-45.
- Сорокин А.С., Математическое моделирование оценки надежности технологических систем // Вестник КузГТУ, 2008 год, №5 (69), Кемерово, С. 28-37.
- Сорокин А.С., Применение методов теории вероятностей к исследованию некоторых процессов производства // Труды 4-ой международной конференции Кибернетика и технологии XXI века Воронеж, 2003 год, С. 312-323.
- Сорокин А.С., Марковские процессы в теории надежности технологических систем гидродобычи угля // Вестник КузГТУ, 2008 год, №1 (65), Кемерово, С 61-69.
- Коэн Дж., Боксма О., Граничные задачи в теории массового обслуживания. М.: МИР, 1987 год.
- Коропюк В.С., Томусяк А.А., Описание функционирования резервированных систем посредством полумарковских процессов // Кибернетика выпуск 5, 1965 год.
- Сорокин А.С., Системы линейных уравнений. Основные понятия анализа Полу марковские процессы // (Гриф УМО) Издательство СибГИУ, Новокузнецк, 1998 год, 151 с.
- Marsan М.А., Donatelli S., Neri F GSPN Models of Markovian Multiserver Multi queue Systems. // Performance Evaluation, 11, 1990.
- Raith T., Performance Analysis of Multibus Interconnection Networks in Distributed Systems // In M. Akiyama, editor, Teletraffic Issues in an Advanced Information Society ITC-11. Elsevier, 1985.
- Morris R.J.T., Wang Y.T., Some Results for Multiqueue Systems with Multiple Cyclic Servers In H. Rudin and W. Bux, editors, //Performance of Computer Communication Systems Elsevier, 1984.
- Kamal A.E., Hamacher V.C., Approximate Analysis of Non-exhaustive Multiserver Polling Systems with Applications to Local Area Networks. //Computer Networks and ISDN Systems, 17(1), 1989.
- Yang Q., Ghosal D., Bhuyan L. Performance Analysis of Multiple Token Pang and Multiple Slotted Pung Networks. // In Proceedings of Computer Network Symposium, Washington DC, 1986.
- Yuk T.I., Palais J.C., Analysis of Multichannel Token Pang Networks // In Proceedings of the International Conference on Communication Systems, 1988.
- Takagi H., Queueing Analysis of Polling Models: An Update. // In H. Takagi, editor, Stochastic Analysis of Computer and Communication Systems. IFIP / North Holland, 1990.
- Choi H., Trivedi K.S., Approximate Performance Models of Polling Systems Using Stochastic Petri Nets // In Proceedings of INFOCOM’92, 1992.
- Ibe O.C., Trivedi K.S., Stochastic Petri Net Models of Polling Systems // IEEE Journal on Selected Areas of Communication, 8(9), 1990.
- Grillo D., Polling Mechanism Models in Communication Systems — Some Application Examples. // In H. Takagi, editor, Stochastic Analysis of Computer and Communication Systems. IFIP / North Holland, 1990.
- Marsan M.A., Donatelli S., Neh F., Rubino U., On the Construction of Abstract GSPNs: An Exercise in Modelling. In J. Billington and W. Henderson, editors, Petri Nets and Performance Modelling // IEEE, December 1991.
- Bunday B.D., Khorram E., The Efficiency of Uni-directionally Patrolled Machines with Two Robot Pepairmen // European Journal of Operational P.esearch, 39(1), 1989.
- Kurkova LA., Malyshev V.A., Martin boundary and elliptic curves // Markov Proc. Relat. Fields. 1998. V. 4 №2. P. 203-272.
- Kurkova I.A., Suhov Yu.M., Malyshev’s theory and JS-queues. Asymptotics of stationary probabilities // A nn. A ppl P robab. 2003. V. 13. № 4. P 1313-1354. 29. Malyshev VA. Networks and dynamical systems. // Adv. Appl. Prob. 1993. V. 25 P. 140-175.
Источник: Моделирование характеристик асимметричной и симметричной систем MSMQ со случайным опросом / А.С. Сорокин // Вестник КузГТУ. 2012 год, №5, страницы 78-84.