Содержание
В системах электроснабжения (СЭС) горных и промышленных предприятий, содержащих преимущественно электродвигательную нагрузку, происходит потребление значительного количества реактивной мощности.
Для обеспечения эффективного энергопотребления и уменьшения потерь мощности возникает необходимость в решении задачи оптимизации процесса компенсации реактивной мощности.
Применения генетического алгоритма для решения задачи оптимизации работы УКРМ
На практике для определения мест расположения и параметров устройств компенсации реактивной мощности, опираются на приближённые методы расчёта потребляемой реактивной мощности, которые учитывают номинальную мощность приемников, номинальный cos ϕ и коэффициент спроса [1,2].
Однако, эти методы не учитывают переходных процессов в СЭС, поэтому имеют существенную погрешность при наличии частых запусков и остановок двигателей, а также при наличии двигателей, имеющих переменную нагрузку.
Использование алгоритмов оптимизации на ЭВМ для определения мощностей устройств компенсации позволяет определить вариант компенсации, при котором потери в СЭС минимальны.
Например, применение генетического алгоритма, основанное на методах расчёта, не учитывающих переходные процессы в СЭС, для задачи компенсации реактивной мощности, рассматривалось в работах [3,4,5].
Подобные способы оптимизации позволяют определить вариант расположения устройств компенсации реактивной мощности.
Математическая модель системы электроснабжения с электродвигательной нагрузкой и устройствами компенсации реактивной мощности [6] учитывает:
- Режимы работы электродвигателей.
- Переходные процессы.
В предложенной математической модели в качестве устройств компенсации используются конденсаторные батареи, которые будут рассматриваться в предлагаемом исследовании.
При использовании алгоритмов оптимизации на основе модели [6] возможно более точно выбрать вариант расположения и параметров устройств компенсации реактивной мощности в СЭС, чем в рассмотренных выше способах.
Задача выбора варианта относится к так называемым задачам переборного типа. Одним из наиболее эффективных алгоритмов поиска оптимального решения в этих случаях является генетический алгоритм [7]. Отметим, что подобный метод использовался в работе [8].
При применения генетического алгоритма к решению задачи оптимизации параметров устройств компенсации реактивной мощности необходимо:
- Выполнить кодирование варианта системы электроснабжения с устройствами компенсации в хромосому.
- Выбрать способы селекции.
- Определить метод скрещивания.
- Определить метод мутации системы.
Далее необходимо определить параметры генетического алгоритма:
- Размер популяции.
- Количество поколений.
- Вероятности скрещивания.
- Вероятности мутации.
Важно выбрать функцию приспособленности (фитнесс-функция) для определения оптимального варианта.
Известно, что по условиям физической реализуемости ёмкость устройства компенсации может принимать конечное множество значений, причем необходимо учесть:
- При этом можно выбрать максимальное значение ёмкости и задать шаг изменения ёмкости, где точность, с которой будет производиться расчёт.
- В этом случае можно определить ёмкость конкретного конденсатора (конденсаторной батареи), который будет максимально близко подходить к вычисленным параметрам.
Вывод формул и алгоритмов расчета для компенсации реактивной мощности в СЭС
Зададим следующие параметры для уравнений:
- Максимальное значение ёмкости, которое может иметь устройство компенсации — Сmax.
- Точность, с которой необходимо определить значение ёмкости устройства компенсации — h.
Тогда ёмкость i-гo устройства компенсации можно записать в виде:

(1)
где
- bi — целое число.
- 0≤bi≤bmax.
- При этом bmax*h≤Cmax.
Таким образом каждому вещественному числу Сi соответствует целое число bi.
Допустим, что в системе электроснабжения существует N мест, где возможна установка устройств компенсации.
Тогда задача оптимизации сводится к определению множества целых чисел b.
Если отсутствует необходимость в устройстве компенсации в том или ином месте, b просто приравнивается к нулю и в расчёте не учитывается.
Теперь представим целое число b в виде последовательности бит следующим образом:

(2)
где
- νi — бит с индексом i в последовательности.
- ɭ — величина последовательности.
Следовательно, получаем следующее выражение:

(3)
Объединив все последовательности, получим одну, состоящую из N*ɭ бит, последовательность, которая и будет служить хромосомой для генетического алгоритма.
Графически хромосома изображена на рисунке 1:
где
- νi1 и νil — соответственно первый, и последний бит в i-ой последовательности, или ген в терминах генетического алгоритма.
Вышесказанное определяет алгоритм вычисления функции приспособленности:
- В процессе оптимизации формируется хромосома — последовательность бит, которая разбивается на N последовательностей по ɭ бит.
- Каждая из последовательностей преобразуется в целое число по выражению.
- Ошибка! Источник ссылки не найден, если не целое число.
- Из полученных целых чисел образуется последовательность ёмкостей по выражению 1.
- Каждому из устройств компенсации в модели присваивается соответствующая ёмкость.
- Производится моделирование полученной системы электроснабжения.
- Из результатов моделирования вычисляется функция приспособленности.
Один из вариантов функции приспособленности это суммарные потери в распределительной сети.
После моделирования и получения зависимости тока от времени на каждом участке распределительной сети.
Следовательно, можно вычислить среднюю величину потерь мощности в сети:
где
- ΔР – мощность.
- M — количество участков распределительной сети.
- i — ток в j-ом участке.
- R — активное сопротивления j-го участка.
Второй вариант, когда определяется срок окупаемости оборудования.
Для этого необходимо посчитать потребление активной мощности в первоначальном варианте и сравнить их с текущей:
где
- Р0 — первоначальное потребление.
- Р1 — потребление активной мощности после компенсации.
Экономия от компенсации составит:

(5)
где
- Э — экономия, зависящая от времени.
- ЦЭ — тариф на электроэнергию
- t — время.
Затраты на установку устройств компенсации:

(6)
где
- 3 – затраты.
- СT — стоимость каждого устройства и его установки.
- m — количество устройств.
С учётом затрат суммарная экономия составит:

(7)
Определим оптимальное количество устройств в СЭС:

(8)
Как видно из уравнения 8, в момент времени t = 0 экономия отрицательная, потому что были приобретены устройства компенсации.
Поэтому имеет место срок окупаемости этого оборудования, когда суммарная экономия достигнет нуля:
- ΔР*ЦЭ*Т-3=0.
Минимизация этого параметра тоже может быть задачей компенсации.
Учитывается вся потреблённая электроэнергия, а не только потери в распределительной сети.
Делается это из соображения, что при различных режимах питания может меняться напряжение на некоторых участках системы электроснабжения, что приведёт к изменению потребляемой мощности самими приёмниками электроэнергии.
Результаты оптимизации одного и нескольких устройств компенсации
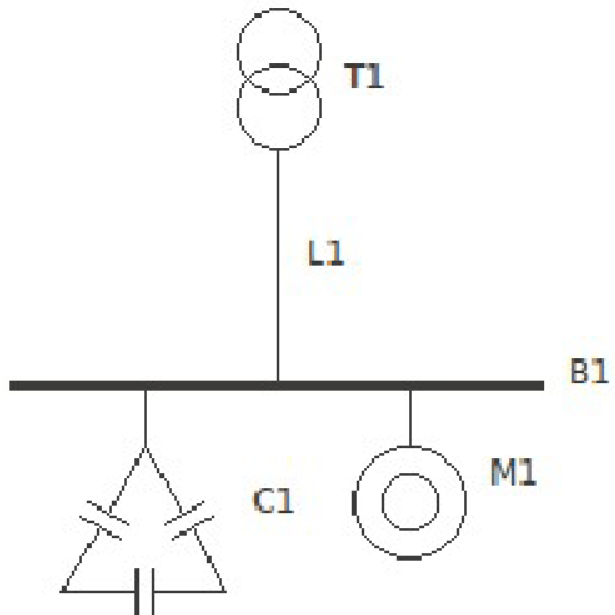
Рассмотрим пример на рисунке 2, одного двигателя, питаемого через кабель от трансформатора:
Необходимо выбрать ёмкость устройства компенсации так, чтобы потери в кабеле были минимальные, в которой используем:
- Электродвигатель ДЕСВ45 с нагрузкой 150 Н-м — вязкое трение.
- Кабель — АПвВГ 4×70 длиной 0,1 км.
Параметры оптимизации:
- Размер популяции – 25.
- Количество поколений – 20.
- Максимальная ёмкость — 1000 мкФ.
- Точность — 1 мкФ.
- Вероятность мутации — 0,05.
- Вероятность скрещивания — 1.
Для реализации алгоритма разработано программное средство, форма с введёнными параметрами оптимизации изображена на рисунок 3, где показана – «0шибка! Источник ссылки не найден»:
В результате оптимизации вычислены следующие параметры и показатели:
- Емкость — 56 мкФ.
- Потери составили 0,304 кВт.
- Без компенсации потери — 0,384 кВт (уменьшились на 80 Вт).
Уменьшение в год составит около 700 кВт-ч или порядка 1,5 миллионов рублей, что при стоимости такого устройства компенсации в несколько десятков тысяч рублей дает значительно.
Рассмотрим вариант с несколькими устройствами компенсации.
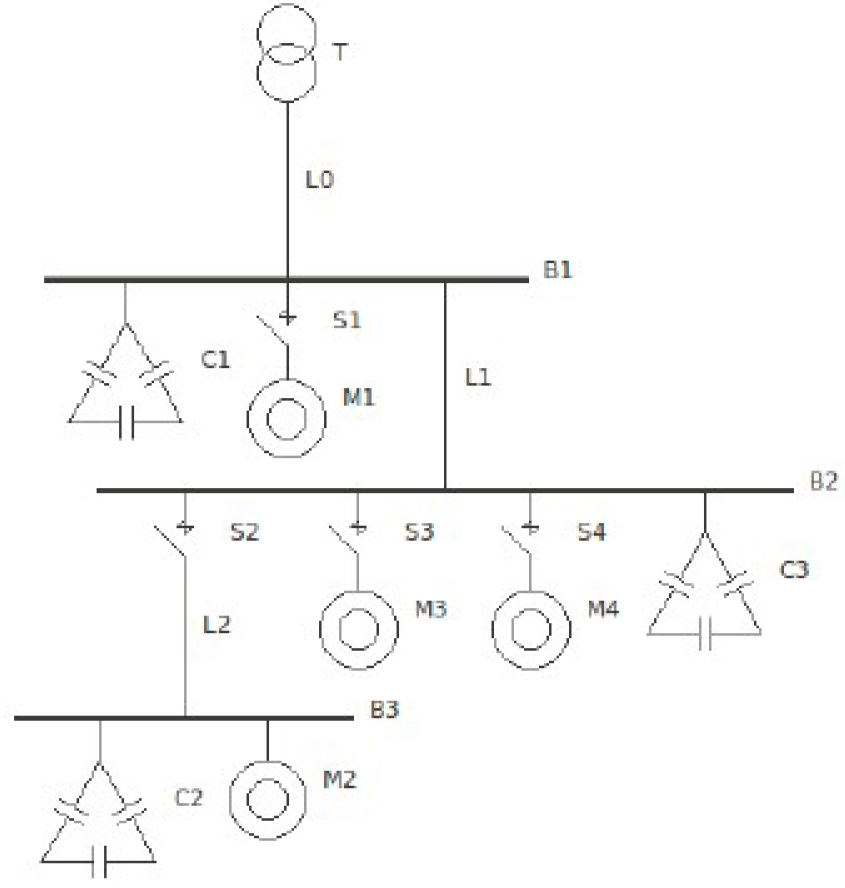
Для примера системы, рассмотренного ранее в [6], произведём оптимизацию с несколькими возможными вариантами размещения устройств компенсации рисунок 4:
Параметры оптимизации:
- Размер популяции – 50.
- Количество поколений – 20.
- Максимальная ёмкость 5000 мкФ.
- Точность — 10 мкФ.
- Вероятность мутации — 0,05.
Значения ёмкостей, полученных после оптимизации:
- С1 =710 мкФ.
- С2=1700 мкФ.
- С3=280 мкФ.
Потери составят:
- 61,15 кВт с компенсацией.
- 99,81 кВт без компенсации.
Результаты компенсации составят:
- Экономия составила 38,66 кВт.
- Суммарная номинальная нагрузка системы составляет 800 кВА.
На основании рассмотренных примеров решений задач, можно сделать следующие выводы:
- Предлагаемый метод оптимизации позволяет учитывать не только расчетную нагрузку, но и переходные процессы, происходящие при запуске и остановке электродвигателей, а также при переменном характере механической нагрузки электродвигателей.
- Из примеров видно, что применение устройств компенсации приводит к значительному уменьшению потерь активной мощности в СЭС.
- В обоих случаях экономия достаточно существенна, так как снижение потерь соизмеримо с самой нагрузкой.
- Генетический алгоритм позволяет добиться наилучшего из возможных вариантов расположения и параметров устройств компенсации реактивной мощности, так как изменение любой ёмкости хотя бы на 1 мкФ в приведенных примерах приводит к увеличению потерь.
Список литературы
- Железко Ю.С., Компенсация реактивной мощности в сложных электрических системах. — Москва: Энергоиздат, 1981. — 200 с.
- Руководящий технический материал «Указания по проектированию установок компенсации реактивной мощности в электрических сетях общего назначения промышленных предприятий» — Москва: ВНИПИ Тяжпромэлектропроект, 1993. — 53 с.
- Управление режимами реактивной мощности и напряжения систем электроснабжения предприятий методами искусственного интеллекта: диссертация кандидата технических наук 05.14.02 / Туликов А.Н. — Красноярск, 2007. 171 с.
- Лоскутов А.Б., Еремин О.И., Многоцелевая оптимизация компенсации реактивной мощности в электрических сетях // Промышленная энергетика. 2006. № б. С. 39-41.
- Optimal Capacitor Placement Using Deterministic and Genetic Algorithms / M. Delfenti, G. Granelli, P. Maranmno, M. Montagna. — IEEE Trans Power Systems, vol. 15, 2000, №3, Aug.
- Математическая модель системы электроснабжения с электродвигательной нагрузкой и устройствами компенсации реактивной мощности.
- Н. Holland, Adaptation in natural and artificial systems University of Michigan Press, Ann Arbor, 1975.
- Негадаев В.А. Определение оптимальных параметров сети электроснабжения с электро двигательной нагрузкой: Диссертация кандидата технических наук / Кузбасский государственный технический университет Кемерово, 2009 г.
Источник: Применение генетического алгоритма для оптимизации параметров устройств компенсации реактивной мощности / В.В. Дабаров // Вестник КузГТУ. — 2012. — №3. — C. 145-147.