Содержание
Производство ряда изделий машиностроения связано с технологическими процессами формообразования геометрически сложных поверхностей деталей.
Эффективное решение задач формообразования поверхностей, обрабатываемых по методу огибания, может быть проведено как с использованием известных методов [1-3] и др., так и с применением методов моделирования средствами компьютерной графики [4-6].
Во втором случае это решение предполагается проводить в два этапа:
- Разработать поверхностную и твердотельную модели детали и представить варианты моделирования удаляемого припуска.
- По результатам моделирования разработать алгоритм и назначить необходимые технологические условия формообразования такой детали наиболее рациональными методами размерной обработки.
Как правило, для обоих этапов существует много решений:
- В первой задаче, независимо от способа решения, должна быть создана одна и та же твердотельная модель заготовки и детали
- Во второй задаче алгоритм и условия формообразования зависят не только от используемых средств компьютерной графики, но и от конкретных процессов обработки.
При этом часто конкретная деталь может быть обработана инструментами одного вида, но с разными формообразующими параметрами:
- Так, например, винтовая поверхность канавки может быть обработана дисковой или червячной фрезой, реечным инструментом и др.
- При этом для одной и той же канавки могут быть использованы различные дисковые инструменты с разными параметрами установки.
- Современные САПР позволяют разработать программы, реализующие движения формообразования в автоматизированном режиме и решать задачи с необходимой точностью [4, 5].
На этапе создания моделей важная роль отводится задаче установления возможных особенностей на исследуемых поверхностях, а также на их отображениях ортогональным проецированием. В некоторых случаях для этих целей важную роль играют вспомогательные поверхности [7], которые определяются через семейство кривых на плоскости.
В настоящей работе рассматриваются три семейства кривых. Они получены в результате перемещения исходной кривой, связанной с окружностью или прямой, катящейся без скольжения по другой окружности или прямой.
Семейство кривых, связанных с окружностью, катящейся по прямой
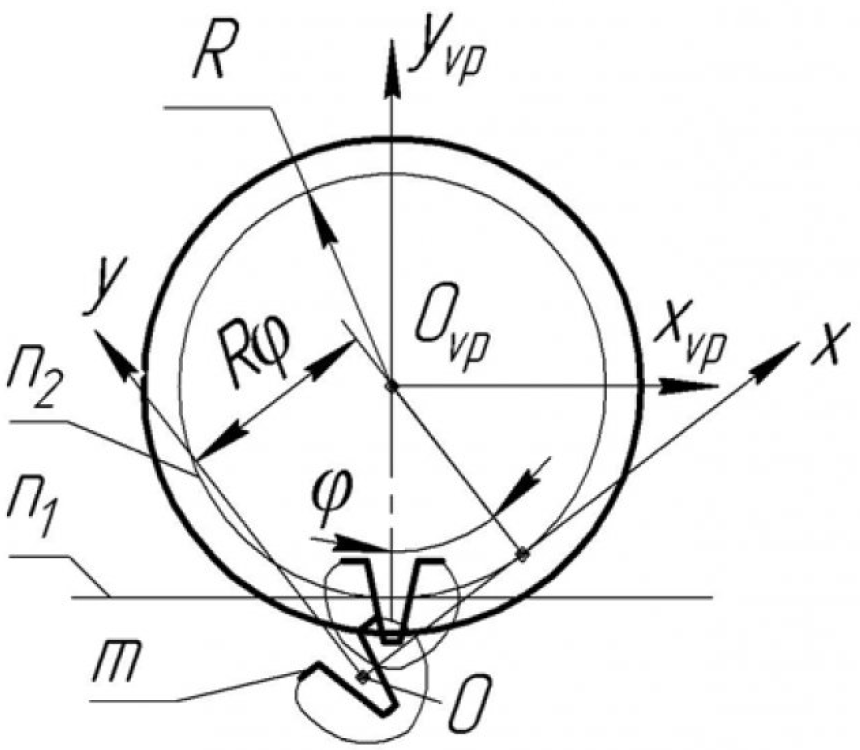
Семейство кривых образуется в результате качения центроиды детали, с которой связана исходная кривая, по начальной прямой инструментальной рейки [7] (рисунок 1):
где
- n1, n2 — центроиды рейки и детали, соответственно.
- m -кривая, связанная с окружностью.
- 0ху — подвижная система координат.
- 0xvpyvpzvp — неподвижная система координат.
Это семейство записывается уравнениями:

(1)
где
- x = x(t) и у = y(t) — уравнения исходной кривой m в подвижной системе координат.
- R -радиус центроиды детали.
Будем рассматривать систему уравнений (1) как график отображения семейства кривых в пространстве R3 на координатную плоскость 0vpxvpyvp(R2).
Тогда это семейство можно записать в виде:

(2)
где
- p — некоторая константа.
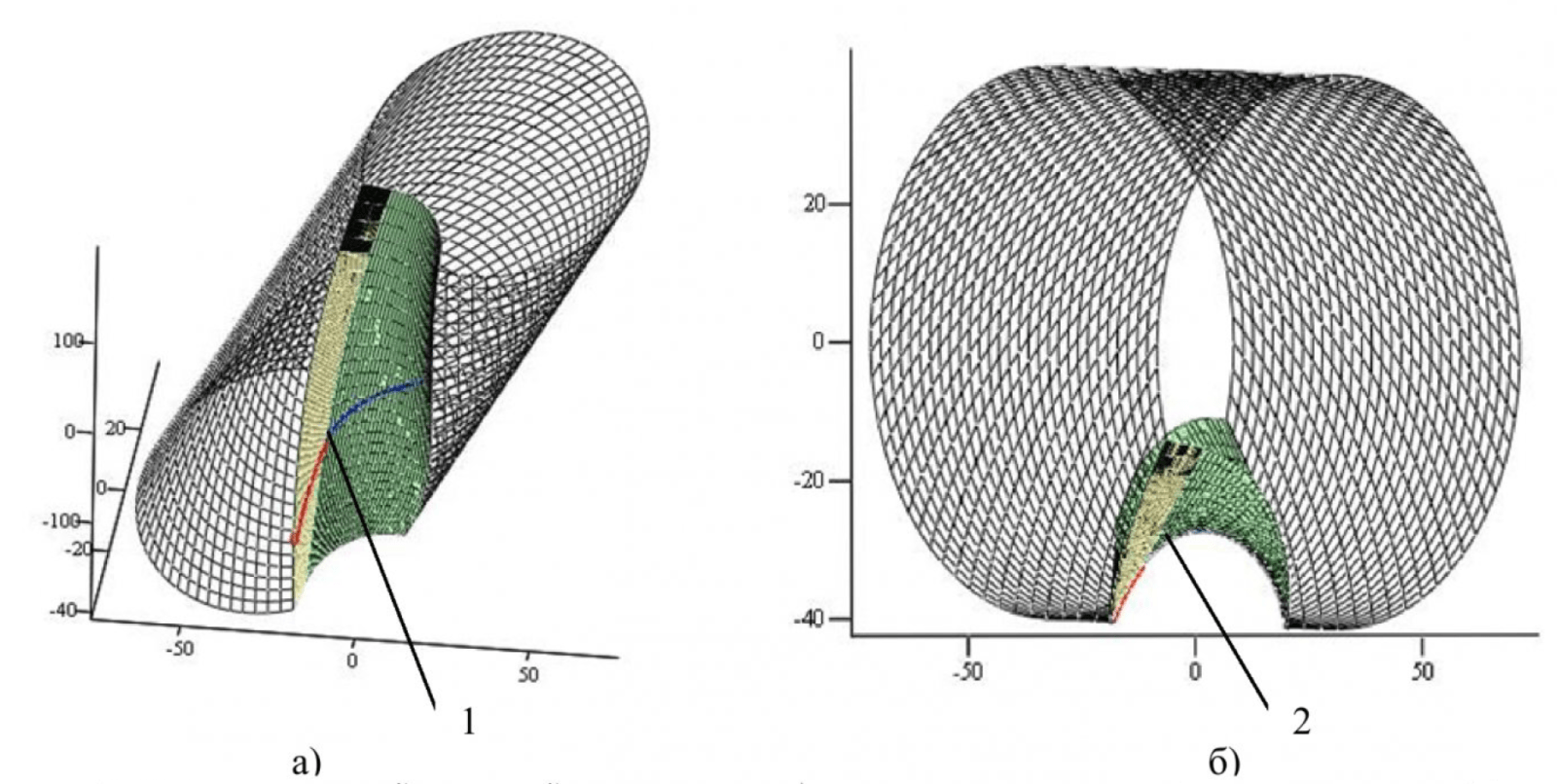
Уравнения такого семейства описывают наклонную винтовую поверхность Ψ, полученную аффинным преобразованием цилиндрической винтовой поверхности (рисунок 2):
где
- а) винтовая поверхность общего положения.
- б) ортогональная проекция винтовой поверхности на плоскость, перпендикулярную оси z.
- 1 — контурная линия поверхности.
- 2 — очерк поверхности (огибающая семейства плоских кривых).
Визуализация такой поверхности средствами системы MathCAD позволяет получить как качественную характеристику самой поверхности (рисунок 2а), так и ее отображения на координатную плоскость 0vpxvpyvp.
Это отображение в локальной окрестности совпадает с огибающей рассматриваемого семейства кривых.
Так как касательные плоскости к поверхности в точках ее контурной линии «вертикальны», то это условие позволяет получить связь параметров t и ϕ в виде:

(3)
Это уравнение определяет некоторую кривую в криволинейных координатах t и ϕ. Отображение этой кривой на поверхность (2) выделяет на ней контурную линию.
Предлагается рассматривать уравнение (3) как уравнение линии нулевого уровня поверхности:

(4)
Такой подход позволяет в системе MathCAD оперативно получать и анализировать графики, определяемые уравнением (3).
Здесь же может проводиться качественный анализ влияния радиуса R центроиды на форму кривой (3), а значит будут устанавливаться возможные особые точки на огибающей рассматриваемого семейства кривых.
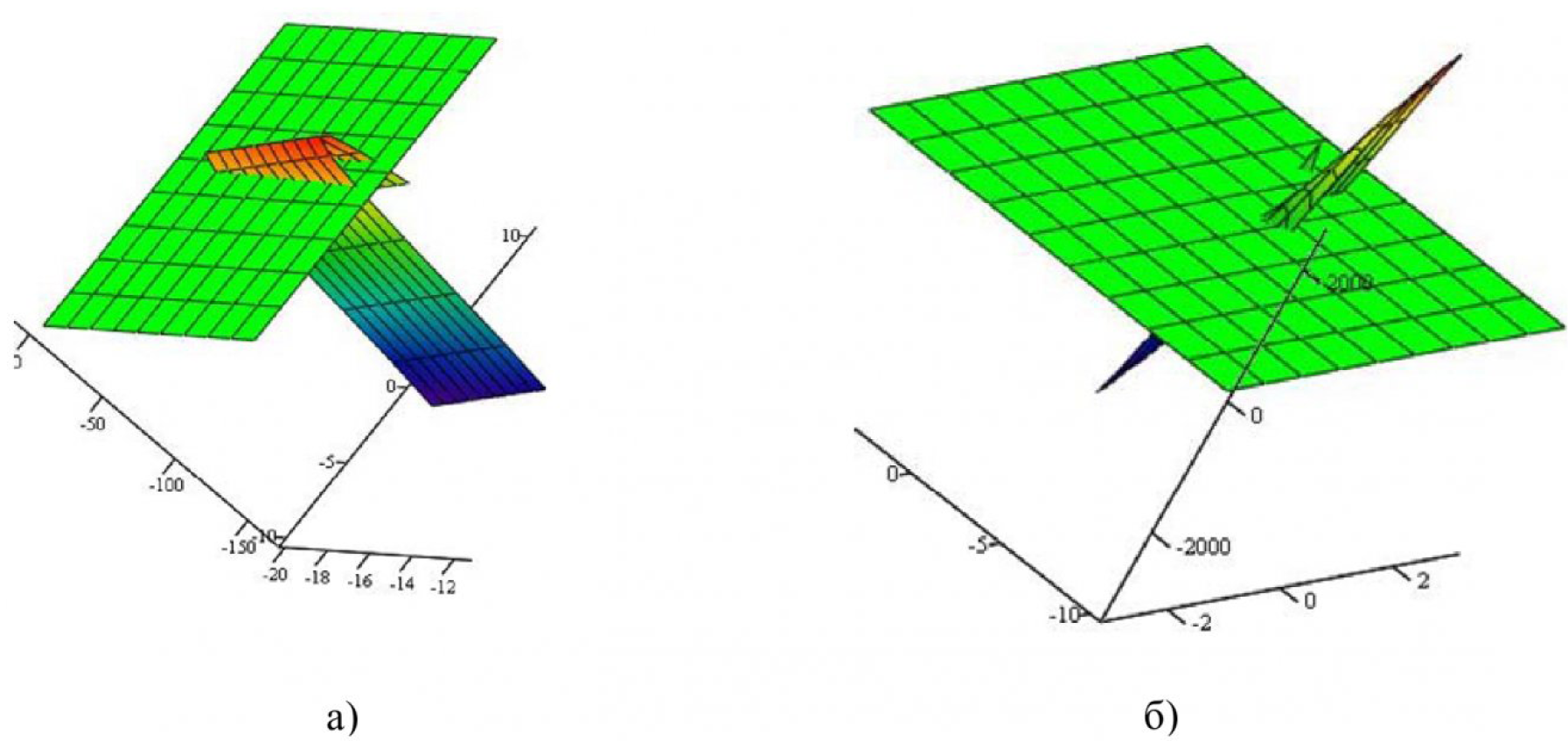
На рисунок 3 показаны графики двух поверхностей, заданных уравнением (4) для случая, когда исходная кривая состоит из двух кусков — отрезка и дуги окружности:
где
- а) для семейства, образованного 1-м участком кривой т.
- б) для семейства, образованного 2-м участком кривой m.
Эти поверхности рассечены плоскостями нулевого уровня, что задает графики связи параметров t и ϕ. С целью подтверждения достоверности полученных результатов.
На рисунке 4 показаны графики тех же кривых, полученных по уравнению (3), но более трудоемких по исполнению:
где
- а) для семейства, образованного 1-м участком кривой т.
- б) для семейства, образованного 2-м участком кривой m.
Семейство кривых, связанных с окружностью, катящейся по другой окружности
Второе семейство кривых образуется в результате качения центроиды детали, с которой связана исходная кривая, по центроиде инструмента (рисунок 5):
где
- n1, n2 — центроиды инструмента и детали, соответственно.
- m — кривая, связанная с центроидой инструмента.
- 0ху — подвижная система координат.
- 0vpxvpyvpzvp — неподвижная система координат.
Это семейство записывается уравнениями:

(5)
где
- x=x(t) и у=y(t) — уравнения исходной кривой в подвижной системе координат.
- ϕ1 — параметр семейства.
В свою очередь где:

Рассматриваем систему уравнений (5) как график отображения семейства кривых в пространстве на координатную плоскость 0vpxvpyvpzvp.
Тогда это семейство можно записать в виде:

(6)
где
- р — некоторая константа.
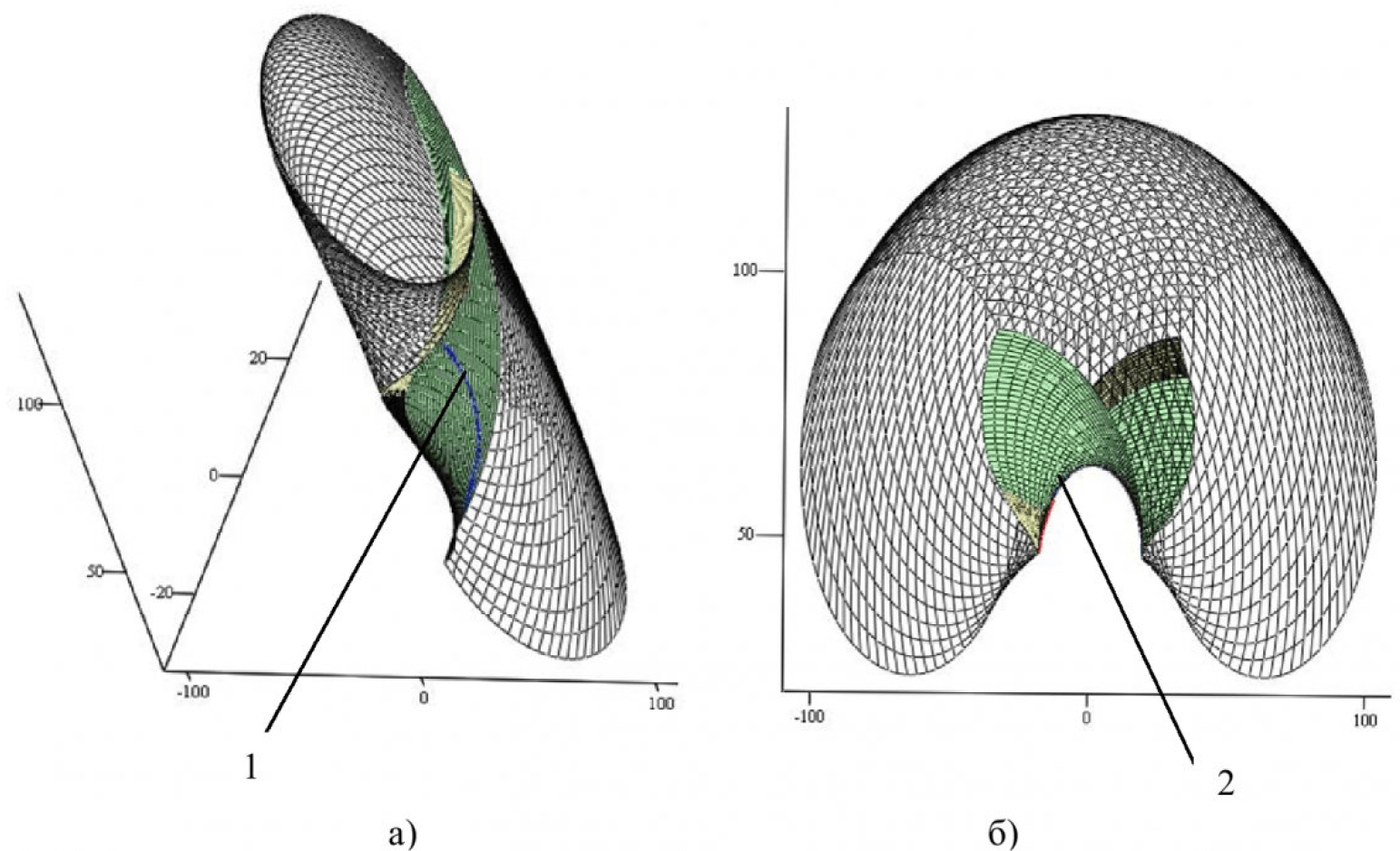
Уравнения такого семейства описывают квазивинтовую поверхность Ω, полученную нелинейным преобразованием цилиндрической винтовой поверхности.
На рисунке 6а эта поверхность показана в общем положении, а на рисунке 66 — в виде ортогональной проекции на координатную плоскость 0vpxvpyvpzvp:
где
- а) квазивинтовая поверхность общего положения.
- б) ортогональная проекция квазивинтовой поверхности на плоскость, перпендикулярную оси z.
- 1 — контурная линия поверхности.
- 2 — очерк поверхности (огибающая семейства плоских кривых).
Как и ранее, предметом визуального исследования является форма очерка поверхности в ее локальной окрестности.
Для получения точных значений координат очерка, а значит и огибающей рассматриваемого семейства кривых, используем уравнение связи параметров t и ϕ вида:

(7)
Это уравнение задает график линии нулевого уровня поверхности, определяемой зависимостью:

(8)
Поверхность (8) и ее сечение плоскостью z(t,ϕ)=0 показаны на рисунке 7:
где
- а) для семейства, образованного 1-м участком кривой m.
- б) для семейства, образованного 2-м участком кривой m.
Семейство кривых, связанных с прямой, катящейся по окружности
Третье семейство кривых образуется в результате качения начальной прямой, с которой связана исходная кривая, по центроиде инструмента (рисунок 8):
где
- n1, n2 — центроиды рейки и детали, соответственно.
- m — кривая, связанная с прямой.
- Оху — подвижная система координат.
- Oxvpyvpzvp — неподвижная система координат.
Это семейство записывается уравнениями:

(9)
По аналогии с изложенным ранее, соответствующая этому семейству квазивинтовая поверхность (рисунок 9):
Определяется уравнениями:

(10)
Связь параметров t и ϕ определяется зависимостью:

(11)
Уравнение поверхности, используемой для визуального исследования связи параметров t и ϕ, имеет вид:

(12)
Приведенные результаты можно рассматривать как первый этап решения задачи формообразования с использованием полигональных моделей вспомогательных поверхностей.
Следующим этапом, позволяющим получить количественные характеристики исследуемых объектов, может быть их твердотельное моделирование с применением известных САПР.
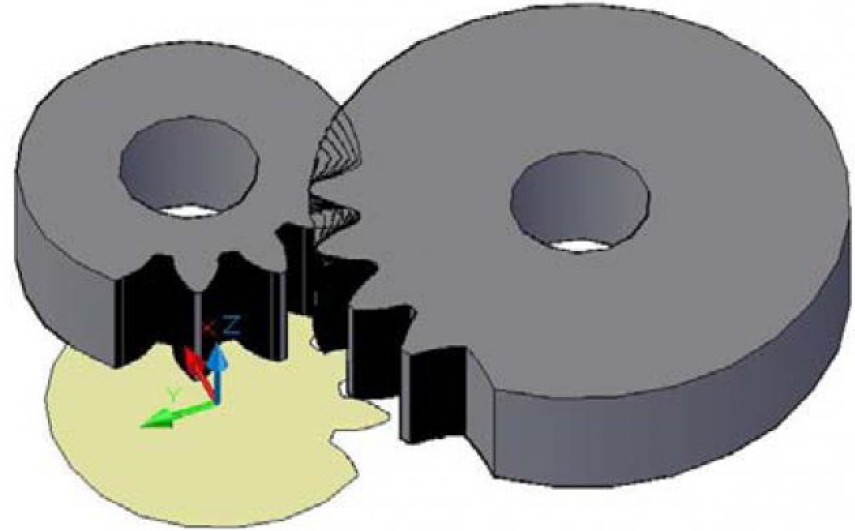
Пример такого моделирования показан на рисунке 10:
Полученная геометрическая и компьютерная модели вспомогательной поверхности позволяет:
- Проводить качественную оценку формы огибающей семейства плоских кривых.
- Оперативно, как дискретно так и в режиме анимации, исследовать влияние радиуса центроиды детали на форму профиля инструмента.
- Корректировать форму профиля детали с последующей визуализацией изменений в профиле инструмента.
Анализ линии нулевого уровня введенных поверхностей, моделирующей график уравнения связи параметров кривой и движения, позволяет установить:
- Границы изменения параметров кривой и движения.
- Возможные особенности как на контуре поверхности, так и на ее очерке, а значит на огибающей семейства плоских кривых.
Так как рассматриваемые кинематические схемы являются не только самостоятельными, но и промежуточными, то приведенные модели применимы при формообразовании различных типов обкаточного инструмента.
Список литературы
- Расчет и конструирование металлорежущих инструментов с применением ЭВМ. / С.И. Лашнев, М.И. Юликов. — М.: Машиностроение, 1975. -392 с.
- Теория винтовых поверхностей в проектировании режущих инструментов. / В.С. Люкшин. — М.: Машиностроение, 1967. — 372 с.
- Обзор методов профилирования червячной фрезы для зубчатых венцов / Н.А. Чемборисов, Т.Г. Девжеева // Металлообработка. — 2010. — № 4. — С. 2-6.
- Моделирование формообразования сложных поверхностей деталей / А.А. Ляшков [и др.] // Металлообработка. — 2010. — № 4. — С. 36-42.
- Программа компьютерного моделирования процесса формообразования зубчатых колес методом обкатки инструментальной рейкой и долбяком./ А.А. Ляшков. — М.: ВНТИЦ, 2008. — № 50200802071.
- Программа компьютерного моделирования процесса формообразования винтовой поверхности детали инструментальной рейкой и червячной фрезой. / А.А. Ляшков. — М.: ВНТИЦ, 2010. -№50201001024.
- Профилирование обкаточного инструмента по вспомогательной поверхности / А.А. Ляшков, Л.К. Куликов // Омский научный вестник. — 1990. — № 9. — С. 73-74.
Источник: Вспомогательные поверхности при моделировании формообразования деталей средствами компьютерной графики / А.А. Ляшков, Ю.А. Канева // Вестник КузГТУ. — 2011. — №5. — C. 75-80.