Содержание
Применяемый в подавляющем большинстве горных и транспортных машин (ГТМ) серийный нерегулируемый электропривод оснащен асинхронными электродвигателями с короткозамкнутым ротором (АД).
Особенностью пуска АД прямым подключением к сети является возникновение знакопеременных переходных электромагнитных моментов, амплитуда которых во многих случаях значительно превышает пусковой момент АД. Так как режим работы электропривода ГТМ характеризуется частыми пусками, то развиваемые АД знакопеременные электромагнитные моменты увеличивают уровень динамической нагруженности электропривода, вызывают удары и деформации в элементах трансмиссии с их интенсивным износом и поломками и являются одной из основных причин, снижающих надежность и ресурс ГТМ.
Одним из направлений повышения функциональной надежности электроприводов ГТМ является управление состоянием приводных электродвигателей при пуске, направленное на ограничение динамических воздействий со стороны электродвигателей на механическую часть ГТМ.
Основными элементами электротехнического комплекса горных и транспортных машин являются трансформатор, питающий кабель и приводные асинхронные электродвигатели. При этом питание электродвигателей осуществляется через протяженную кабельную сеть, в которой при пуске АД происходит увеличение падения напряжения со снижением напряжения на вторичной обмотке трансформатора.
Помимо этого, на переходный процесс пуска АД также влияет характер момента сил сопротивления на валу электродвигателя, зависящий от нагрузки конкретного типа машины. Эти факторы необходимо учитывать при исследовании динамических процессов в электроприводе ГТМ при пуске и анализе эффективности способов управления пуском асинхронного электропривода.
Метод исследования динамических процессов
Основным методом исследования динамических процессов в электроприводе ГТМ является компьютерное моделирование. Максимальное приближение результатов компьютерного моделирования к реальным динамическим процессам в электроприводе ГТМ.
Получение правильной оценки эффективности способов управления пуском приводных электродвигателей возможно при использовании интегрированной математической модели электрических компонентов электротехнического комплекса ГТМ в составе:
- Трансформатора.
- Кабельной сети.
- Устройства управления пуском, асинхронного электродвигателя.
Переменные состояния первичной и вторичной цепи трехфазного трансформатора, а также кабельной сети определяются системами дифференциальных уравнений, приведенными в [1]:

где
- RsT, RrT — активные сопротивления первичной и вторичной обмоток трансформатора.
- ѰsТА, ѰsTB, ѰsTC — потокосцепления фаз первичной обмотки трансформатора.
- ѰrТА, ѰrTB, ѰrTC — потокосцепления фаз вторичной обмотки трансформатора.
- usТА, usTB, usTC — фазные напряжения первичной обмотки трансформатора.
- urТА, urTB, urTC — фазные напряжения вторичной обмотки.
- isТА, isTB, isTC — фазные токи первичной обмотки трансформатора.
- irТА, irTB, irTC — фазные токи вторичной обмотки трансформатора.
- Rk, Lk — активное и индуктивное сопротивления кабельной сети.
- ukA, ukB, ukC — падения напряжения в фазах кабельной сети.
- ikA, ikB, ikC — фазные токи кабельной сети.
Для формирования интегрированной математической модели электрических компонентов электротехнического комплекса ГТМ модель АД, приведенную в [1], удобно представить в виде системы, записанной в неподвижной относительно статора системе координат α, β:

где
- isA, isB, isC, usA, usB , usC — фазные токи и напряжения статора.
- Rs, Rr — активные сопротивления обмоток статора и ротора.
- σ = 1 — Lm / LsLr — коэффициент рассеяния.
- Lm — взаимная индуктивность между статорной и роторной обмотками.
- Ls, Lr — индуктивности обмоток статора и ротора.
- р — число пар полюсов.
- ω — частота вращение ротора.
- Мэм — электромагнитный момент, развиваемый электродвигателем.
Составляющие тока статора (isα, isβ) и потокосцепления ротора (Ѱrα, Ѱrβ) по осям α, β, а также величины еrA, еrB, еrC определяющие ЭДС, наводимую вращающимся магнитным потоком ротора в фазах статора, определяются в соответствии с выражениями по [2]:

При этом состояние тиристорных коммутационных элементов (ТКЭ), а, следовательно, фаз статорной обмотки определяется разностью потенциалов между нулевыми точками звезды напряжений источника питания и звезды напряжений электродвигателя — u0:

При непроводящем состоянии ТКЭ, например фазы А, величина u0 будет определяется выражением (еrА + uB + uC)/2, при непроводящем состоянии ТКЭ в двух фазах (А и В) – u0 = еrА + erB + uC.
где
- uA, uB, uC — фазные напряжения источника питания.
Выразив уравнения, описывающие состояния первичной и вторичной обмоток трансформатора через составляющие потокосцепления первичной обмотки в неподвижных ортогональных осях α, β — ѰsTα, ѰsTβ и фазные токи вторичной обмотки — irТА, irTB, irTC, после преобразования получим интегрированную математическую модель электрических компонентов электротехнического комплекса ГТМ.
Модель включает в себя описание силового трансформатора, кабельной сети, устройства управления пуском и асинхронного электродвигателя:

где
- LsT, LrT — индуктивности первичной и вторичной обмоток трансформатора.
- LmT — взаимная индуктивность между первичной и вторичной обмотками трансформатора.
- σТ = 1 — LmT / LsTLrT — коэффициент рассеяния трансформатора.
- usTα, usTβ — составляющие напряжения первичной обмотки трансформатора по осям α и β.
- u0 — напряжение между нулевыми точками вторичной обмотки трансформатора и статорной обмотки электродвигателя.
Величина u0 во всех фазах при проводящем состоянии тиристоров определяется в соответствии с выражением:
- u0 = (esTA +esTB + esTC)/3
При непроводящем состоянии тиристора в одной фазе, например в фазе А, справедливо:
- u0 = (esTB +esTC + erA)/2
Данная модель получена с учетом того, что напряжение на зажимах электродвигателя равно напряжению на зажимах вторичной обмотки трансформатора за вычетом падения напряжения в кабельной сети:

В свою очередь модель с учетом равенства токов в фазах трансформатора, силового кабеля и электродвигателя будет:

Величины егА, егВ, егC и ток статора в осях α, β определяются в соответствии с вышеприведенными выражениями, а величины esTA, esTB, esTC — по выражениям:

Данная модель справедлива не только для случая применения тиристорных коммутационных элементов, но и при использовании в силовой схеме полностью управляемых полупроводниковых приборов, так как состояние статорной обмотки определяется величиной u0, которая, в свою очередь, при компьютерном моделировании задается программной:
- В зависимости от условий переключения коммутационных элементов (условия существования тока в цепи с коммутационными элементами).
- От выбранного типа управления (фазовое, квазичастотное, широтноимпульсное — при использовании полностью управляемых полупроводниковых приборов).
Применение модели на практическом примере
При дополнении интегрированной модели математической моделью рабочего органа конкретной машины (рисунок 1) появляется возможность исследовать эффективность выбранного способа пуска её приводных электродвигателей.
где
- Трансформатор.
- Кабельная сеть.
- Устройство управления пуском.
- Асинхронный электродвигатель.
- Рабочий орган скребкового конвейера.
Рассмотрим вопрос управления пусковыми режимами электропривода скребкового конвейера (СК), для которого проблема благоприятного пуска является особенно острой. Для этой цели воспользуемся описанием рабочего органа СК, приведенным в [3].
Математическая модель рабочего органа СК при этом представляется в виде совокупности отдельных элементарных звеньев, которые состоят из трех элементов:
- Масса (mk).
- Упругий элемент с коэффициентом упругости равным ky.
- Демпфирующий элемент, обусловленный действием сил вязкого трения, с коэффициентом вязкого трения равным kв.т. (рисунок 2).
На каждую массу элементарного звена (k-й элемент) действуют:
- Упругие силы со стороны соседних элементов fk-1=ky(xk-1-xk-L0) и fk+1=ky(хk-xk+1-L0).
- Силы внешнего (сухого) трения fmp(νk), зависящие от скорости перемещения звена νk.
- Тангенциальная составляющая силы тяготения fm=mg*sinβ, величина которой определяется положением конвейера (углом наклона става конвейера — β).
- Сила реакции опоры N (става конвейера).
Правомерность подобного подхода к описанию рабочего органа СК обусловлена тем, что при движении рабочего органа происходит концентрация перемещаемого груза в районе скребков (рисунок 3), поэтому принимаем, что суммарная масса mk (цепь, скребок, груз) распределяется не равномерно по длине элементарного звена L0, а сосредоточена в одной его зоне.
При такой постановке задачи, уравнения движения рабочего органа скребкового конвейера будут иметь следующий вид:

где
- xk, νk, mk — координата, скорость движения и масса k-oro элемента (рисунок 2 и рисунок 3)
- L0 — длина элементарного звена
Получим усилие, передаваемое со стороны приводного электродвигателя, задаётся через начальную координату х0 системы:

где
- ip — передаточное отношение редуктора.
- mпр — приведенная масса вращающихся частей привода.
- Rпp — радиус приведения.
В этих уравнениях не представлено действие сил вязкого трения, так как в первом приближении их влиянием на характер протекания динамических процессов при управляемом пуске асинхронного электропривода ГТМ можно пренебречь.
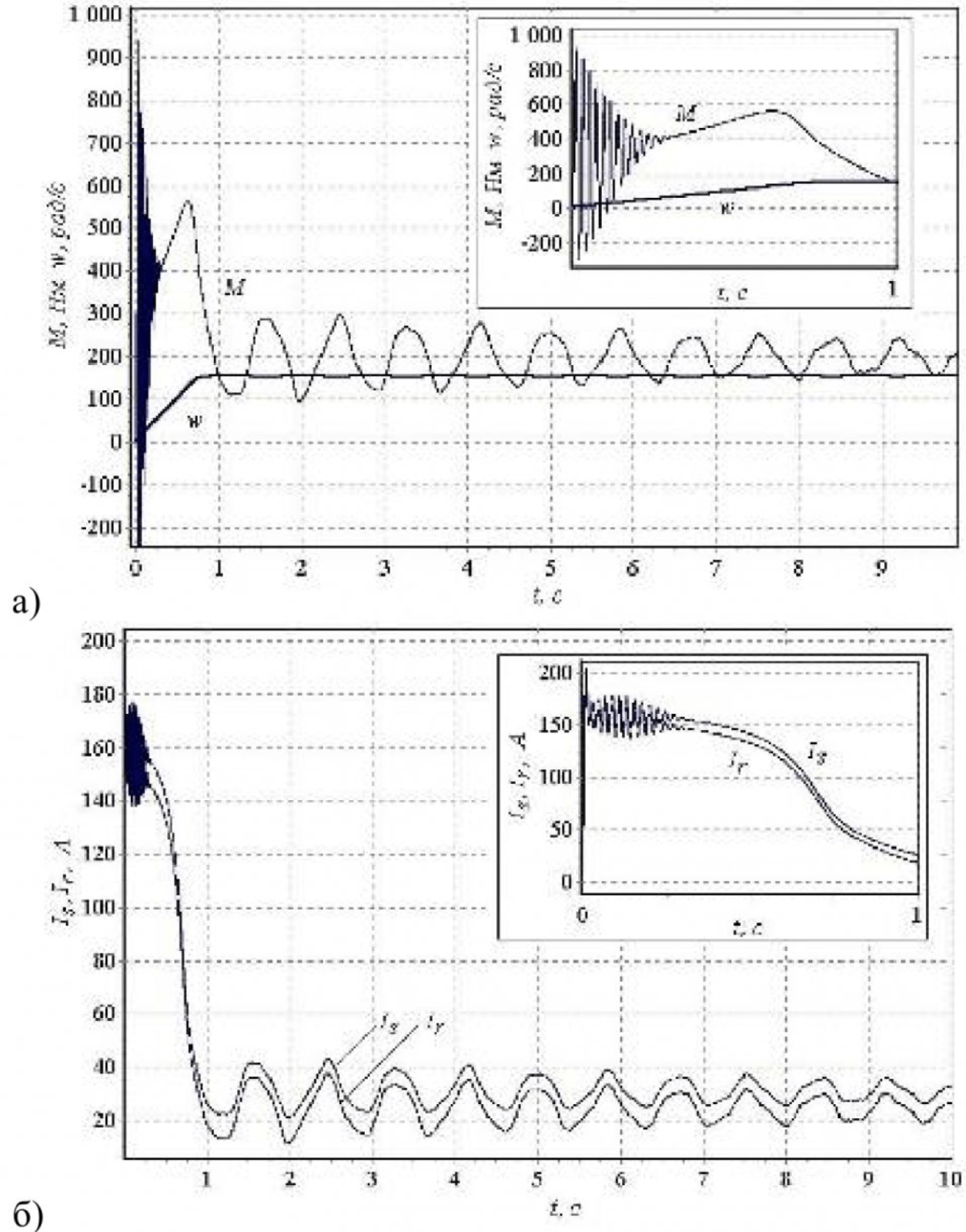
На рисунке 4 представлены графики изменения момента, частоты вращения ротора и тока в обмотках статора и ротора при пуске электродвигателя скребкового конвейера прямым подключением к сети, полученные при компьютерном моделировании.
где
- а) — электромагнитный момент (М) и частота вращения (ω).
- б) — токи в обмотках статора (Is) и ротора (Ir).
Использовались следующие параметры:
- Длина конвейера — 100 м.
- Калибр цепи — 18×64.
- Масса одного метра цепи со скребками — 18 кг.
- Масса груза — до 50 кг/м.
- Передаточное отношение редуктора ip – 20.
- Рабочий орган приводится в движение асинхронным электродвигателем ДКВ45.
Как видно из рисунка, приводной электродвигатель развивает значительные по величине знакопеременные электромагнитные моменты, приводящие к опасным механическим напряжениям в трансмиссии и тяговой цепи конвейера.
При этом пусковые токи в обмотках электродвигателя достигают величин, в несколько раз превосходящих номинальные значения, что негативным образом сказывается на состоянии лобовых частей статорной обмотки.
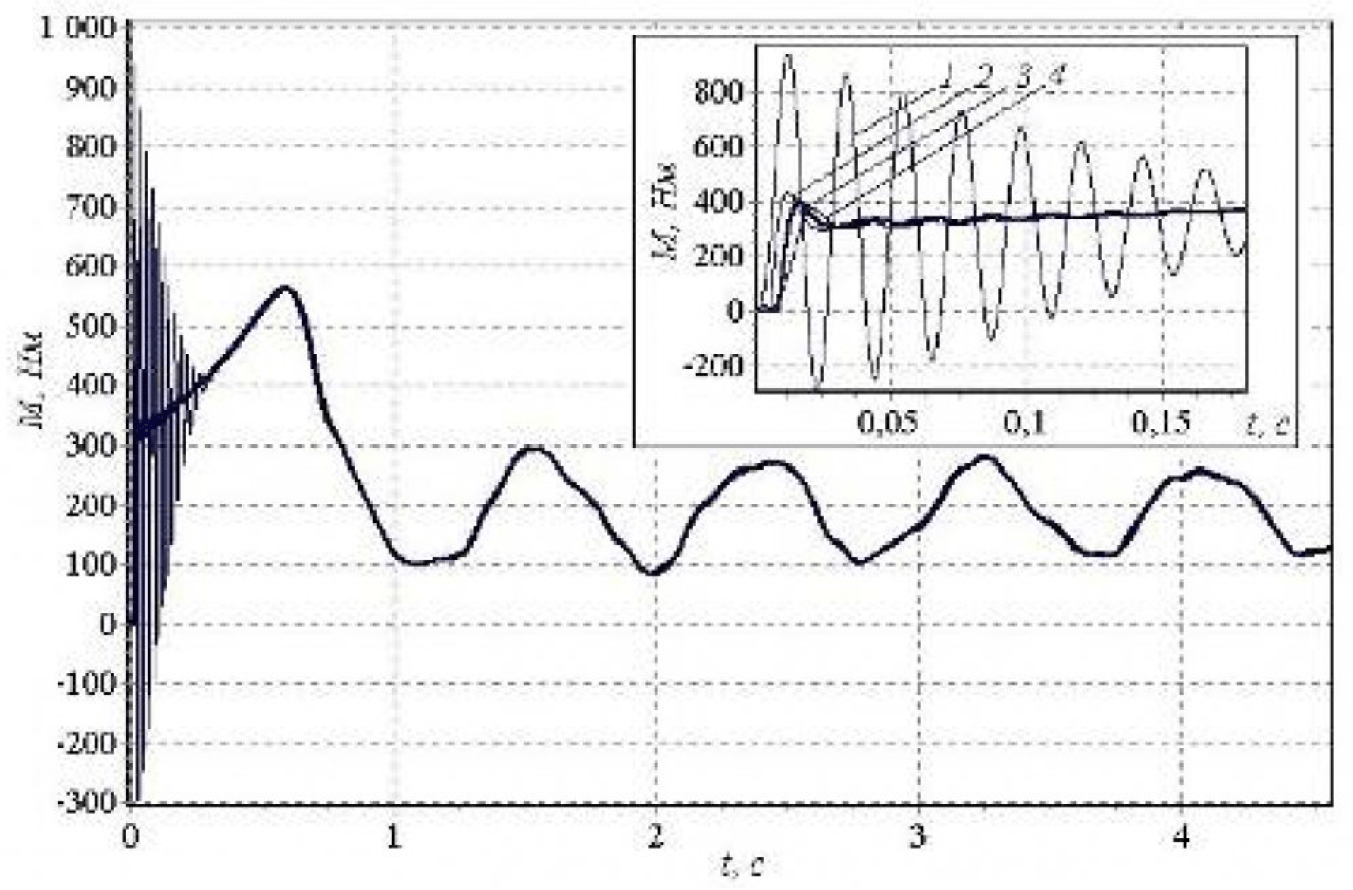
На рисунке 5 приведены переходные моменты при моделировании управляемого пуска АД:
- Пофазный пуск [4].
- Квазиоптимальный пуск [5].
- ШИМ- пуск [6].
где
- При прямом пуске (1).
- При квазиоптимальном пуске (2).
- При пофазной подаче напряжения (3).
- При ШИМ пуске (4).
Очевидно, что управляемый пуск АД значительно снижает динамическую составляющего тока Iу.у.п по сравнению с прямым пуском (смотрите рисунок 6).
где
- а) ударное значение электромагнитного момента.
- б) ударное значение пускового тока.
- в) энергия электрических потерь
Приведенные здесь номера соответствуют отмеченным способам пуска на рисунке 5.
Результаты компьютерного моделирования управляемого пуска приводного электродвигателя СК также показали, что за счет ограничения пускового тока и уменьшения длительности переходного процесса достигается снижение энергии электрических потерь в АД (рисунок 6в).
Таким образом, повышение функциональной надежности асинхронных электроприводов ГТМ возможно при переходе к управляемому пуску. Для экспериментальной проверки нами было разработано универсальное транзисторное устройство управляемого пуска АД, испытания которого подтвердили приведенные здесь результаты компьютерного моделирования.
Список литературы
- Копылов И.П. Математическое моделирование электрических машин. — М.: Высшая школа, 2001. -327 с.
- Моделирование асинхронных электроприводов с тиристорным управлением / Л.П. Петров, В.А. Ладензон, Р.Г. Подзолов, А.В. Яковлев. — М.: Энергия, 1977. — 200 с.
- Бандурин, А.Н. Моделирование динамики рабочего органа скребкового конвейера // Вести. Кузбасского гос. тех. унив., 1999. — №2. — С. 46-49.
- Петров Л.П. Управление пуском и торможением асинхронного двигателя. — М.: Энергоиздат, 1981.- 184 с.
- Способ пуска асинхронного электродвигателя / Е.К. Ещин, В.Г. Каширских, И.А. Соколов, С.С. Переверзев // Математические методы в технике и технологиях — ММТТ-18: Сб. трудов 18-й Междуна-род. науч. конф.: в 10 т. Т.5. Секция 5 / Под общ. ред. В.С. Балакирева. — Казань: изд-во Казанского гос. технол. ун-та, 2005. — С. 200 — 204.
- Формирование алгоритма управления плавным пуском асинхронного электродвигателя на основе метода скоростного градиента / В.Г. Каширских, В.М. Завьялов, С.С. Переверзев // Вести. Кузбасского гос. тех. унив., 2005. — № 2 — С. 7 — 9.
Источник: К вопросу формирования математической модели для исследования эффективности способов управления пуском горных и транспортных машин / С.С. Переверзев, А.В. Нестеровский // Вестник КузГТУ. — 2010. — №6. — C. 79-85.