Особенностью работы горных машин, осуществляющих выемку горной массы из забоя, являются тяжелые условия их эксплуатации, в результате чего для них характерны относительно частые поломки механических элементов.
Статистика аварийных простоев горных машин показывает, что их существенная доля связана с выходом из строя элементов трансмиссии главных приводов. Так, длительность простоев карьерных экскаваторов, вызванных ликвидацией поломок элементов трансмиссии, составляет более 50 % от общего времени аварийных простоев [1], а на элементы трансмиссии угледобывающих комбайнов приходится около 25 % от всех отказов [2]. Все это ведет к существенным экономическим убыткам горнодобывающих предприятий.
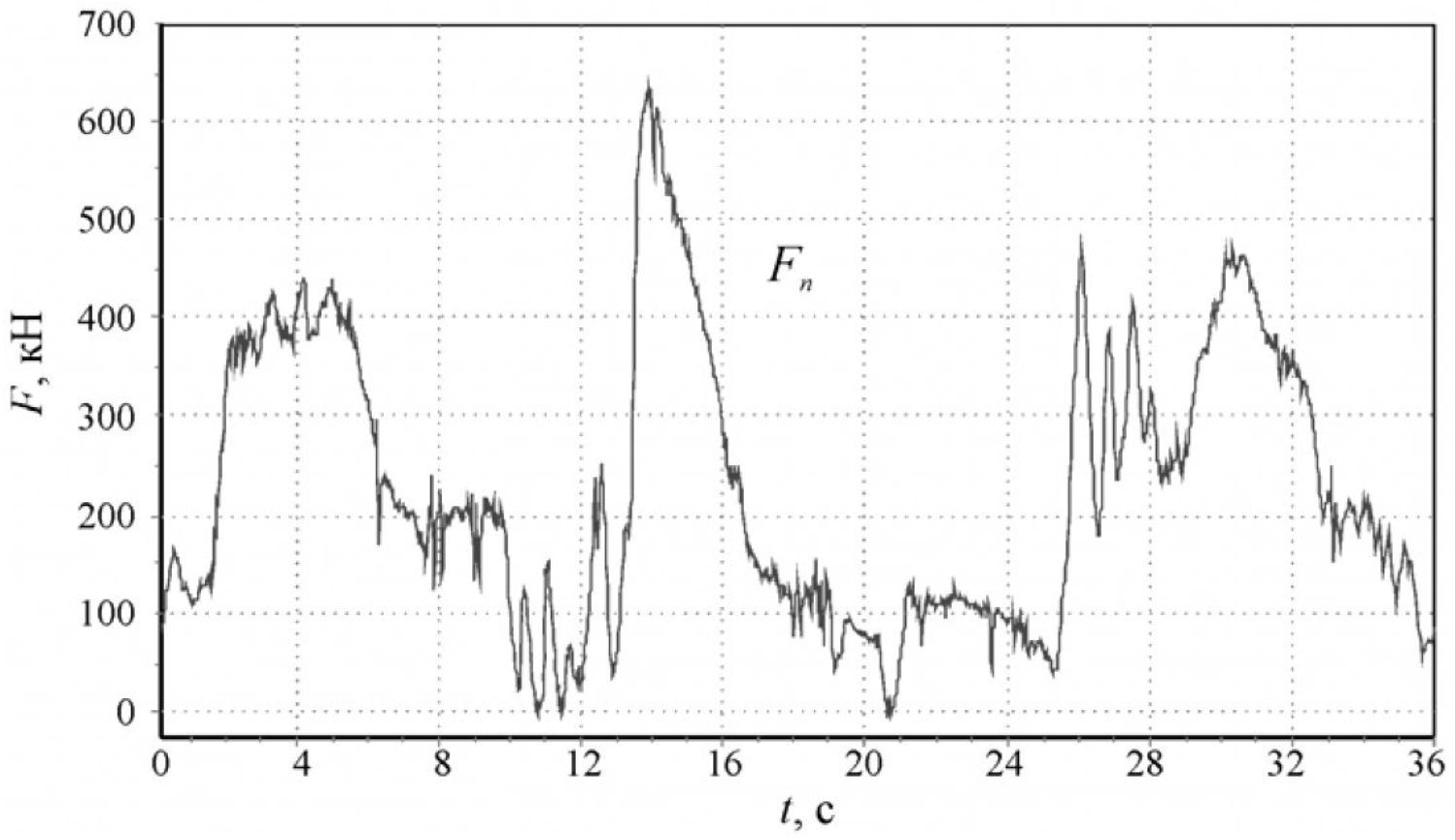
Основная причина отказов механических элементов вызвана тем, что электроприводы горных машин преодолевают нагрузку, изменяющуюся во времени случайным образом. В результате, при работе горных машин в их трансмиссиях постоянно протекают переходные процессы. В конечном итоге это вызывает переменную составляющую нагрузки действующей на элементы трансмиссии, как это показано на рис. 1, способствующей накоплению в них усталостных повреждений, и, в конечном итоге, выходу их из строя.
Для снижения уровня переменной составляющей нагрузки, действующей на элементы трансмиссий горных машин, наряду с конструктивными решениями, позволяющими оптимизировать конструкцию механических передач, например, как это предлагается в [2], возможно также использовать регулируемый электропривод.
По второму направлению имеется большое количество работ, посвященных исследованию демпфирующих свойств электропривода, на основании чего предлагается оптимизировать параметры системы управления электроприводом по критерию демпфирующей способности [3]. Также известны работы, в которых исследуются системы управления с различными видами обратных связей с точки зрения их влияния на демпфирующую способность регулируемого электропривода и предлагаются критерии их настройки [4, 5].
Большинство работ в этом направлении опирается на модель линеаризованной электромеханической системы, которой в наибольшей степени соответствует электропривод на базе двигателя постоянного тока с независимым возбуждением. В последние годы в промышленности все в большей степени отказываются от электропривода постоянного тока в пользу асинхронного частотно-регулируемого электропривода, что вызвано с одной стороны низкой надежностью машин постоянного тока, обусловленной наличием щеточно-коллекторного аппарата, а с другой — интенсивным развитием преобразовательной и микропроцессорной техники.
Для электроприводов горных машин так же наиболее перспективным является полностью управляемый асинхронный электропривод, о чем было отмечено еще в 70-х годах в работе [6]. Алгоритмы управления такими электроприводами для отдельных типов горных машин, способствующие улучшению их динамического состояния, приведены в работах [7-9].
Таким образом, для перевода горных машин на новый технический уровень необходима разработка и внедрение регулируемых асинхронных электроприводов, система управления которых обеспечивала бы помимо совершения полезной работы, направленной на разрушение горного массива, управление динамическим состоянием их механических подсистем с целью исключения переменной составляющей нагрузок, действующих на элементы трансмиссии, вызванной взаимодействием рабочего органа горной машины с забоем.
Структура системы управления
Особенностью асинхронных электроприводов горных машин является то, что их силовой канал, как объект управления, является достаточно сложной системой. С одной стороны асинхронный двигатель является нелинейным объектом с внутренними связями и изменяющимися параметрами, с другой стороны — механические передачи для различных горных машин отличаются по структуре, и как следствие, имеют различные математические модели, которые также могут быть нелинейными.
В связи с этим, при разработке алгоритмов управления такими электроприводами целесообразно использовать подход, заключающийся в декомпозиции системы на отдельные подсистемы, решении локальных задач управления для каждой отдельной подсистемы, а затем агрегировании отдельных подсистем при условии требуемого движения полной системы.
Разделение системы электропривода горной машины осуществим по физическому признаку на электрическую и механическую подсистемы. При этом электрическую подсистему, включающую в себя асинхронный двигатель, питаемый от автономного инвертора напряжения с использованием полеориентированного, прямого или градиентного управления моментом, можно рассматривать как безынерционный источник момента [10].
В этом случае можно рассматривать задачу управления динамическим состоянием механических подсистем электроприводов горных машин как независимую, считая, что управляющим воздействием, которое будет формировать система управления, является момент сил на входе механической подсистемы.
Основным критерием регулирования механических координат горных машин является обеспечение их требуемой интегральной производительности. Средняя годовая или месячная производительность горной машины зависит с одной стороны от средней скорости движения исполнительного органа, а с другой — от соотношения времени работы к времени внеплановых простоев.
Учитывая, что внеплановые простои, вызванные поломкой элементов трансмиссии горной машины, во многом зависят от протекающих в них динамических процессов, задача управления динамическим состоянием механических подсистем электроприводов горных машин сводится к управлению скоростью движения исполнительного органа, и управлению силами, действующими на элементы механической подсистемы горной машины.
При представлении математической модели механической подсистемы в виде системы с сосредоточенными параметрами, силы действующие на элементы трансмиссии, будут пропорциональны упругим силам и упругим моментам.
Таким образом, для регулирования механических координат система управления должна включать в свой состав регуляторы упругого момента и скорости, как это показано на рис. 2, где используются следующие обозначения:
- PC — регулятор скорости
- РУМ — регулятор упругого момента
- БИМ — безынерционный источник момента
- МП — механическая подсистема электропривода
- ω*, ω -заданное и текущее значения угловой скорости рабочего органа
- М*1,2 — заданное значение упругого момента
- М*, М — заданное и текущее значение электромагнитного момента двигателя
- Мс -момент сопротивления
- YМ — вектор механических координат электропривода.
Требования к регуляторам
Рассмотрим особенности синтеза регуляторов для данной системы на примере механической подсистемы, представленной двухмассовой расчетной схемой. Математическая модель такой системы с одной стороны является наиболее простой, а с другой стороны, во многих случаях, сложные механические передачи трансмиссий горных машин могут быть упрощены до двухмассовой [11].
Математическая модель двухмассовой системы имеет вид:

(1)
где
- ω1, ω2, J1, J2 — угловые скорости и моменты инерции первой и второй масс
- М1,2 — упругий момент
- С1,2 — коэффициент жесткости упругой связи
Анализируя второе уравнение системы (1), описывающее движение рабочего органа горной машины, можно увидеть, что при изменяющемся моменте сопротивления невозможно одновременно стабилизировать угловую скорость рабочего органа и величину упругого момента. Учитывая, что средняя интегральная производительность горной машины зависит от средней скорости движения исполнительного органа на некотором интервале времени, можно ослабить требования к точности регулирования скорости путем выделения диапазона ее допустимого изменения. Для этого необходимо разделить пространство состояний на две области, как это показано на рис. 3.
Для достижения цели управления необходимо добиться согласованной работы регуляторов механических координат таким образом, чтобы при нахождении изображающей точки в области I она стремилась попасть в область II, а при нахождении в области II упругий момент поддерживался на заданном уровне, не реагируя на изменения угловой скорости, вызванные изменяющейся нагрузкой. Помимо этого, движение изображающей точки к области I должно осуществляться по достаточно гладкой траектории без периодической составляющей.
Решение этой задачи возможно путем ее разделения на задачу регулирования момента и задачу регулирования скорости. Используя при этом методы синергетической теории управления [12] для синтеза алгоритма управления упругим моментом, гарантирующего движение изображающей точки к инвариантному многообразию, соответствующему цели управления с последующим движением вдоль него, алгоритм управления угловой скоростью будет полностью определять динамическое состояние механической подсистемы.
Регулятор упругого момента
Для поддержания упругого момента на заданной траектории, введем желаемое инвариантное многообразие:

(2)
Очевидно, что задав М*1,2=const, при выходе системы на инвариантное многообразие упругие колебания будут отсутствовать. В тоже время, изменяя М*1,2, можно воздействовать на ускорение механической системы, а значит и на ее скорость.
Решив для инвариантного многообразия (2) функциональное уравнение:

где
- Т1 — постоянная времени, определяющая скорость движения изображающей точки к инвариантному многообразию (2)
Подставив в него правую часть третьего уравнения системы (1) и приняв М*1,2=const, получим следующее уравнение:

(3)
В полученном уравнении отсутствует подводимый к двухмассовой механической системе момент сил М, являющийся управляющим воздействием. Для устранения этого недостатка введем в систему внутреннее управление, в качестве которого выберем угловую скорость первой массы.
Выберем следующее желаемое инвариантное многообразие для внутреннего управления:

где
- ʋ — желаемая траектория движения переменной ω1, полученная из (3)

Таким образом, получаем следующее инвариантное многообразие, движение по которому позволяет поддерживать упругий момент M1,2 на заданном уровне:

(4)
Решая уравнение, получим:

где
- Т2 — постоянная времени, определяющая скорость движения изображающей точки к инвариантному многообразию (4)
Сделав преобразования уравнений (1) и (4), получим алгоритм управления:

(5)
При этом изображающая точка из любого положения в фазовом пространстве попадет на инвариантное многообразие (2), после чего будет двигаться вдоль него.
Регулятор скорости
Произведем синтез регулятора скорости, основываясь на уравнении движения второй массы двухмассовой системы, представленном в виде:

(6)
Согласно (6), величина упругого момента уравновешивается моментом сопротивления и динамическим моментом, вызванным изменением угловой скорости рабочего органа, исходя из чего задание упругого момента должно определяться требуемым ускорением рабочего органа при известном текущем значении момента сопротивления.
При таком подходе к формированию задания упругого момента в трансмиссии, учитывая основные требования, предъявляемые к регулятору скорости, желаемое ускорение рабочего органа при нахождении угловой скорости в области допустимых отклонений, должно быть равно нулю, а задание упругого момента должно соответствовать среднему значению момента сопротивления. В этом случае изменения угловой скорости будут происходить только под действием переменной составляющей нагрузки MСvar, а значение угловой скорости рабочего органа не будет выходить за пределы установленных допустимых отклонений.
В случае изменения задания угловой скорости, ее значение может оказаться за границами области допустимых отклонений. Тогда регулятор скорости должен перевести ее в заданный диапазон за минимальное время. В этом случае задание упругого момента необходимо формировать с учетом динамического момента, соответствующего максимально допустимому ускорению.
Таким образом, алгоритм регулятора скорости должен реализовывать зависимость:

где
- Мдин* — требуемое значение динамического момента, необходимого для изменения угловой скорости.
При нахождении ω2 в области II (рис. 3) значение Мдин* должно быть равно нулю, а за ее пределами обеспечивать требуемое ускорение. Регулятор, реализующий данную зависимость, далее будем называть адаптивным компенсационным регулятором скорости.
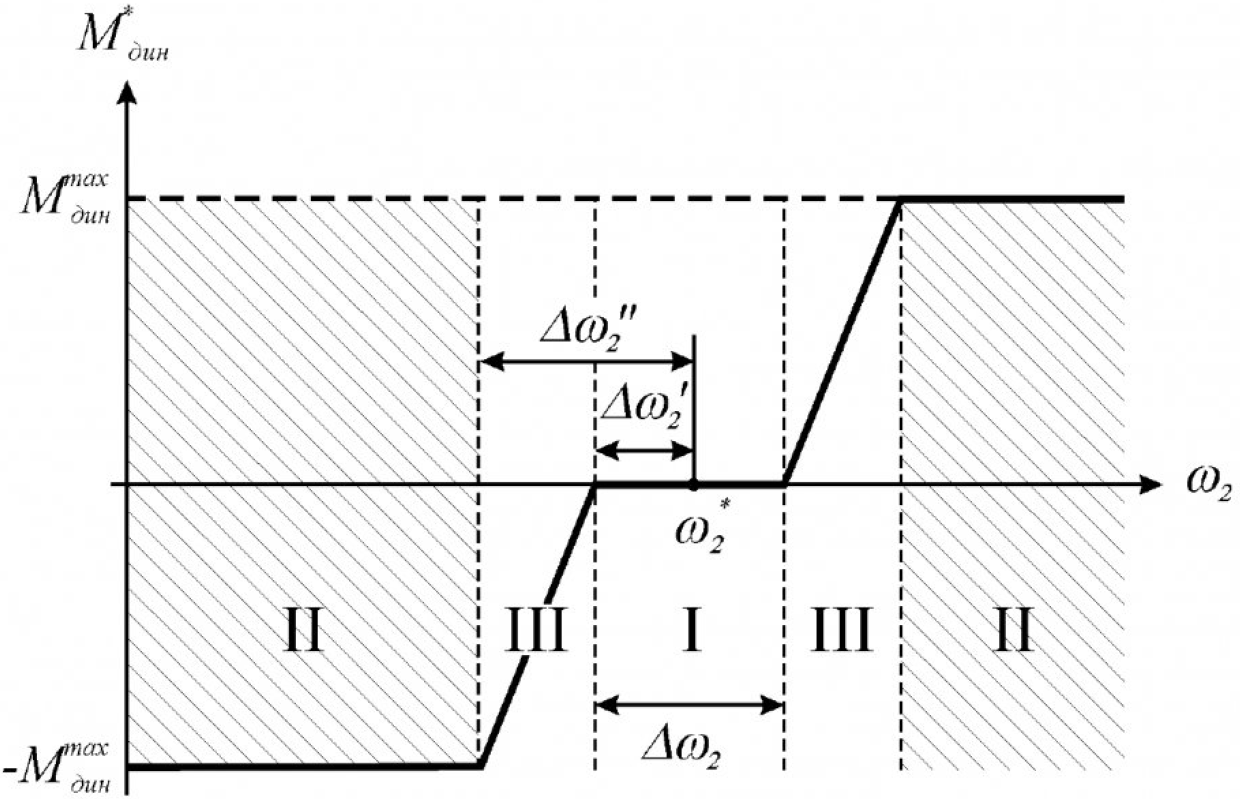
Если во всей области I (рис. 3) поддерживать постоянное ускорение, то при переходе ω2 в область II, задание упругого момента будет изменяться ступенчато, что может привести к возникновению автоколебаний. Возможность возникновения такого режима можно исключить, если в пространстве состояний ввести дополнительную область III, как это показано на рис. 4, при движении по которой динамический момент снижается от максимально допустимого значения до нуля по мере приближения к области II.
В этом случае требуемый динамический момент, в зависимости от текущего значения угловой скорости, будет определяться как:

где
- ω2* — заданное значение угловой скорости рабочего органа.
Для реализации данного регулятора необходимо исключить высокочастотную составляющую момента сопротивления и определить его среднее значение. Это можно осуществить, используя фильтр низких частот.
Величина зоны I регулятора скорости
Диапазон изменения ω2 при М1,2=const будет определяться переменной составляющей нагрузки, а значит, будет зависеть от вероятностных свойств момента сопротивления. Поскольку при M1,2=const будет соблюдаться равенство ω1= ω2, а следовательно, равенство Δω1 = Δω2, рассмотрим связь ширины области Δω1, в которой допускается изменение частоты вращения ω1.
Запишем уравнение движения первой массы двухмассовой системы:

С учетом алгоритма управления упругим моментом (5), это выражение запишется как:

Учитывая, что при стабилизации упругого момента ω1 — ω2 = 0 и M1,2 — M1,2* = 0 получим:

(7)
Принимая во внимание, что работа горной машины в установившемся режиме должна проходить при условии M1,2≈m(МC).
где
- m(МC) — математическое ожидание момента сопротивления
Делаем преобразование уравнения и тогда (7) примет вид:

(8)
где
- МCvar — переменная составляющая нагрузки.
Полученное уравнение движения первой массы, при выборе в качестве входного воздействия момента сопротивления, является уравнением интегрирующего звена.
Зная спектральную плотность момента сопротивления, можно определить дисперсию выходного сигнала [13], которым в нашем случае является угловая скорость первой массы:

где
- Dω1 — дисперсия угловой скорости первой массы
- SMc(Ω) — спектральная плотность момента сопротивления
- A(Ω) — амплитудно-частотная характеристика, которая для (8) будет иметь вид:

Таким образом, дисперсия угловой скорости первой массы будет определяться выражением:

Далее, зная дисперсию угловой скорости первой массы, для нее можно определить плотность распределения вероятности, используя закон распределения вероятности момента сопротивления.
В результате, задавшись желаемой вероятностью нахождения угловой скорости в заданной области, можно определить границы этой области.
Так, при нормальном законе плотности распределения вероятности при Δω1=2σω1
где
- σω1 — среднеквадратичное отклонение угловой скорости от ее математического ожидания
Вероятность нахождения угловой скорости в заданной области будет равна Pω1= 0,68
- При Δω1 = 4σω1 — Pω1 = 0,95
- А при Δω1=6σω1 — Pω1 =0,997
По аналогии можно распространить полученный вывод на механические системы с большим числом выделенных масс.
Результаты исследования
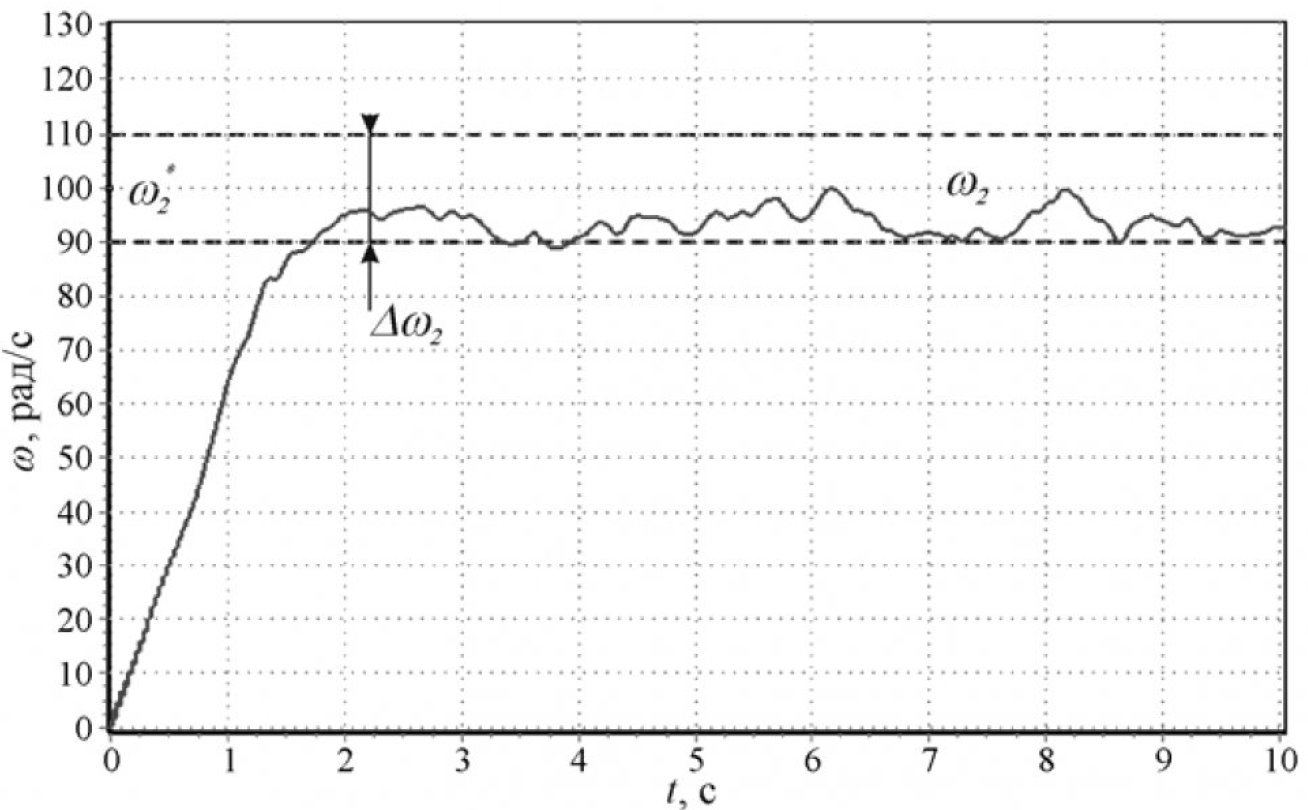
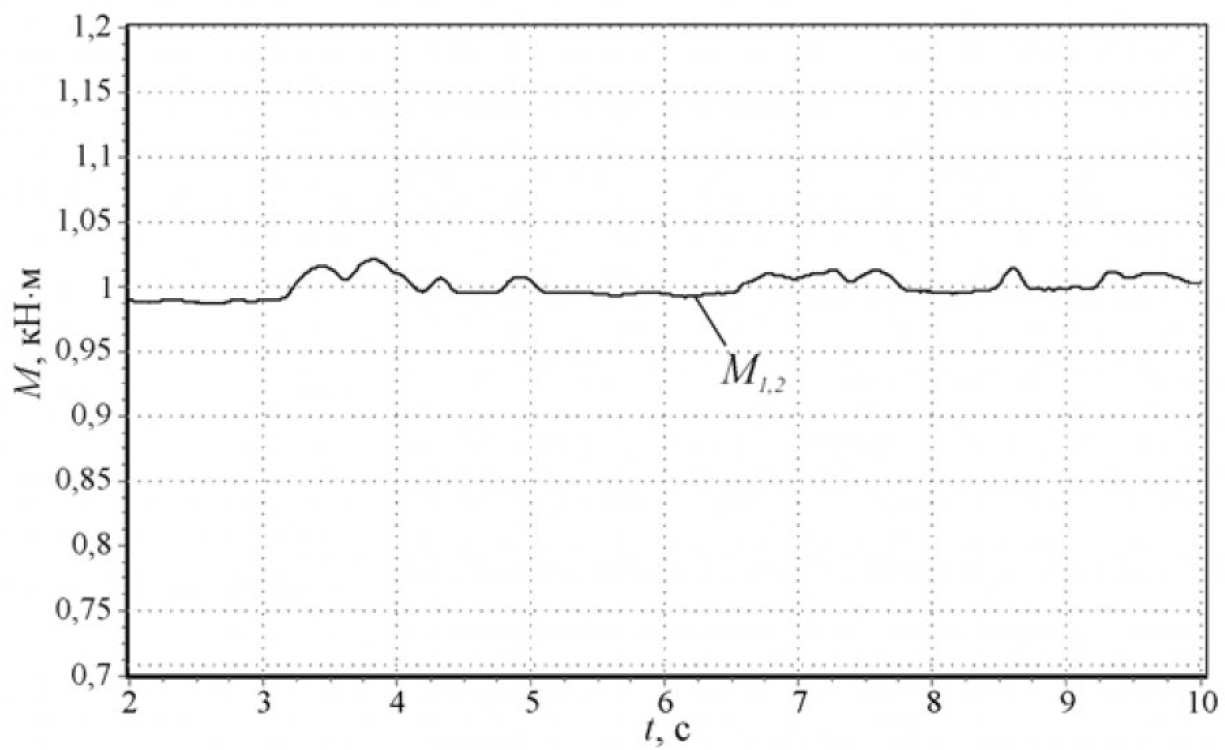
Исследование разработанных алгоритмов управления механическими координатами электроприводов горных машин осуществлялось с использованием компьютерного моделирования с параметрами объекта управления, соответствующими электроприводу резания очистного комбайна Eickhoff SL 300. Результаты моделирования приведены на рис. 5 и рис. 6.
Для сравнения, на рис. 7 показаны результаты моделирования этого электропривода в неуправляемом варианте при тех же внешних условиях.
Анализ результатов показывает, что использование разработанных алгоритмов управления позволяет уменьшить до 12 раз амплитуду колебаний упругих моментов в элементах трансмиссии без выхода угловой скорости рабочего органа за границы допустимого диапазона.
Повышение эксплуатационной надежности горных машин возможно путем управления динамическим состоянием механических передач с использованием регулируемого электропривода на базе асинхронного электродвигателя, выполняющего функцию безынерционного источника момента.
Разработанные алгоритмы управления механическими координатами позволяют существенно снизить амплитуду переменной составляющей нагрузки, действующей на элементы трансмиссии горной машины, а значит, увеличить срок безотказной работы элементов и горной машины в целом.
Список литературы
- Завьялов, В.М. Анализ отказов карьерных экскаваторов / В.М. Завьялов, И.Ю. Семыкина // Природные и интеллектуальные ресурсы Сибири. Сибресурс 2006: Материалы XI Международной научно- практической конференции, 23-24 нояб. 2006. — Кемерово: КузГТУ, 2006. — С. 179-180.
- Иванов, С.Л. Повышение ресурса трансмиссий горных машин на основе оценки энергонагруженности их элементов. — СПб.: Санкт-Петербургский горный ин-т, 1999. — 92 с.
- Ключев, В.И. Состояние и перспективы развития теории электропривода с упругими механическими связями / В.И. Ключев, Л. В. Жильцов, Ю.Т. Колашников // Электричество. — 1981. — № 7. — С. 28-32.
- Ляхомский, А.В. Управление электромеханическими системами горных машин / А.В. Ляхомский, В.Н. Фащиленко. — М.:МГГУ, 2004. — 296 с.
- Пятибратов, Г.Я. Возможности применения электроприводов для активного ограничения колебаний упругих механических передач // Изв. вузов. Электромеханика. — 1990. — № 10. — С. 89-93.
- Тулин, В.С. Современная научно-техническая революция и развитие электропривода // Изв. вузов. Горный журнал. — 1970. — № 4. — С. 86-90.
- Гаврилов, П.Д. Снижение уровня динамической нагруженности скребкового конвейера при помощи асинхронного электропривода / П.Д. Гаврилов, Е.К. Ещин // Изв. вузов. Горный журнал. — 1978. — № 1 1 .- С . 99-105.
- Ещин, Е.К. Теория предельных режимов работы горных машин. — Томск: ТГУ, 1995. — 232 с.
- Бабокин, Г.И. Система управления электроприводом с упругим звеном переменной жесткости // Горное оборудование и электромеханика. — 2007. — № 1. — С. 47-48.
- Завьялов, В.М. Безынерционный источник момента на базе асинхронного электропривода / В.М. Завьялов, И.Ю. Семыкина // Автоматизированный электропривод и промышленная электроника в металлургической и горно-топливной отраслях: Труды третьей Всероссийской научно-практической конференции, 16-18 мая 2006. — Новокузнецк: СибГИУ, 2006. — С. 121-124.
- Красников, Ю.Д. Оптимизация привода выемочных и проходческих машин / Ю.Д. Красников, 3.Я. Хургин, В.М. Нечаевский и др. — М.: Недра, 1983. — 264 с.
- Современная прикладная теория управления: синергетический подход в теории управления / Под ред. А.А. Колесникова. — Таганрог: ТРТГУ, 2000. — Ч.П. — 559 с.
- Лукас, В.А. Теория автоматического управления техническими системами. — Екатеринбург: УГ- ГА, 2002. — 675 с.
Источник: Ресурсосберегающее управление электроприводами горных машин / В.М. Завьялов // Вестник КузГТУ. — 2010. — №1. — C. 93-99