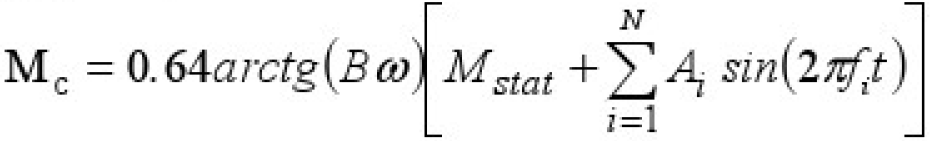Содержание
Перевод электрической машины из одного состояния в другое — классическая задача управления, которая была освещена в ранних статьях [1,2].
Формирование уравнения для управления позиционированием электродвигателя
При этом минимально необходимые уравнения движения электропривода можно записать с естественными ограничениями в виде:
где
- y — угол поворота вала ротора электродвигателя (ЭД), в обозначениях на рисунках – Gamma.
- ω — частота вращения ротора асинхронного электродвигателя АД.
- ΔМ=М-МС — динамический момент (в обозначениях на рисунках — DeltaM).
- М — электромагнитный момент ЭД.
- МС — момент сопротивления на валу ЭД.
- J — момент инерции.
Формулировка задачи в постановке, например, о переводе объекта из произвольного начального состояния в начало координат (y=0, ω=0) физически означает возврат к нулевому значению угла поворота ротора и остановку вращения ЭД.
Этот вариант управления можно представить себе в машинах, у которых по условиям выполнения технологического процесса исполнительный орган должен вернуться в исходное положение.
Существует также задача об обеспечении электроприводу конечных условий, когда:
- y=yz.
- ω=0.
где
- yz — задаваемое значение угла поворота ротора ЭД — задача позиционирования.
Подобные рода задачи возникают, например, при управлении электроприводами запорной арматуры, а также во многих других задачах финитного управления.
Рассмотрим решение задачи позиционирования по условию обеспечения максимального быстродействия при переходе системы электропривода из одного состояния в другое и изменяющейся нагрузке на валу электродвигателя.
Где учитываются следующие условия:
- Управляющее воздействие при позиционировании — динамический момент (ДМ).
- В качестве исполнительного двигателя примем асинхронный электродвигатель (АД) с его математической моделью по [3].
Запишем для исходной системы в соответствии с принципом максимума Л.С. Понтрягина [4] вспомогательную функцию Н:

В силу условий обеспечения максимума для Н будем иметь:
Отсюда следует, что оптимальное управление является функцией, принимающей значения ΔМmах, ΔMmin и имеющей не более двух интервалов постоянства [4].
По отношению к электромагнитному моменту (М) АД его необходимое (задаваемое) значение определится как:
- MZ=ΔМ+МС.
Это уравнение обеспечивается при постоянстве динамического момента будет определяться только величиной момента сопротивления.
Таким образом, возникает задача перевода электропривода из одного состояния в другое за минимум времени при изменяющейся нагрузке, что эквивалентно обеспечению классических фазовых траекторий перемещения по [4].
Из исходной системы уравнений движения можно записать:

При этом необходимо обеспечить условие:
Уравнение поверхности (линии) переключения [7- 9] будет выглядеть так:
Следовательно, при управлении со стороны статора в координатной системе α, β примет вид:
Разработка программного обеспечения для полученного уравнения
После получения системы уравнений, результаты решения задачи сформируем в среде MatLab SimuLink.
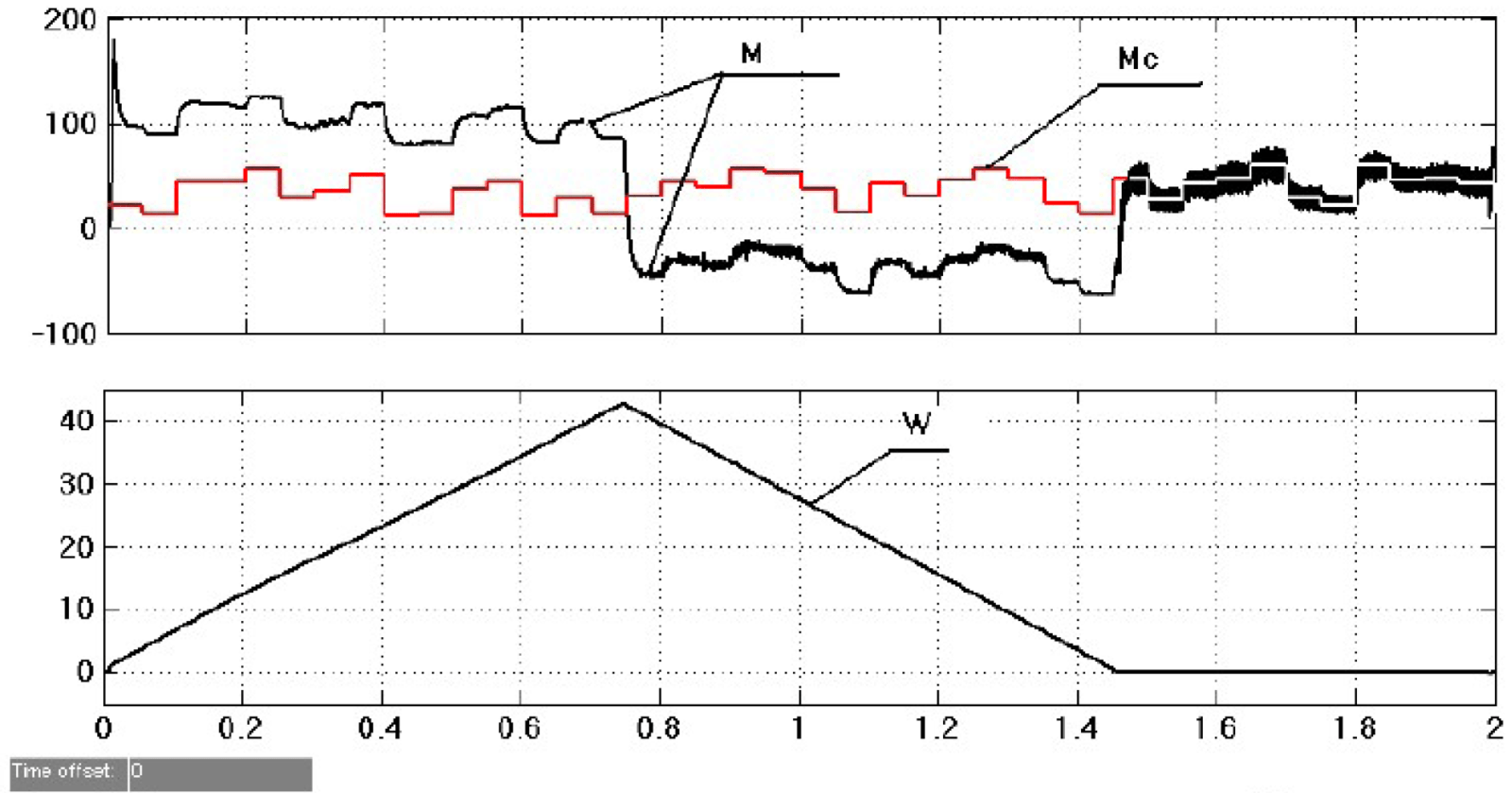
Решение задачи показано на рисунке 1:
В виде траекторий изменения координат приведены на рисунке 2:
где
- Электромагнитного момента АД.
- Скорости вращения ротора (нижний график).
- При обеспечении постоянства динамического момента при повороте ротора АД на угол 4π.
- Моделирование произведено в среде Matlab Simulink.
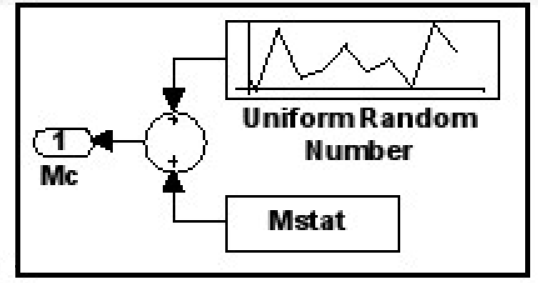
Формирование величин момента сопротивления (активного) для модели в Matlab Simulink проводилось совокупностью блоков, показанных на рисунке 3:
Формирование МС реактивного для модели в среде Delphi на основании следующего уравнения:
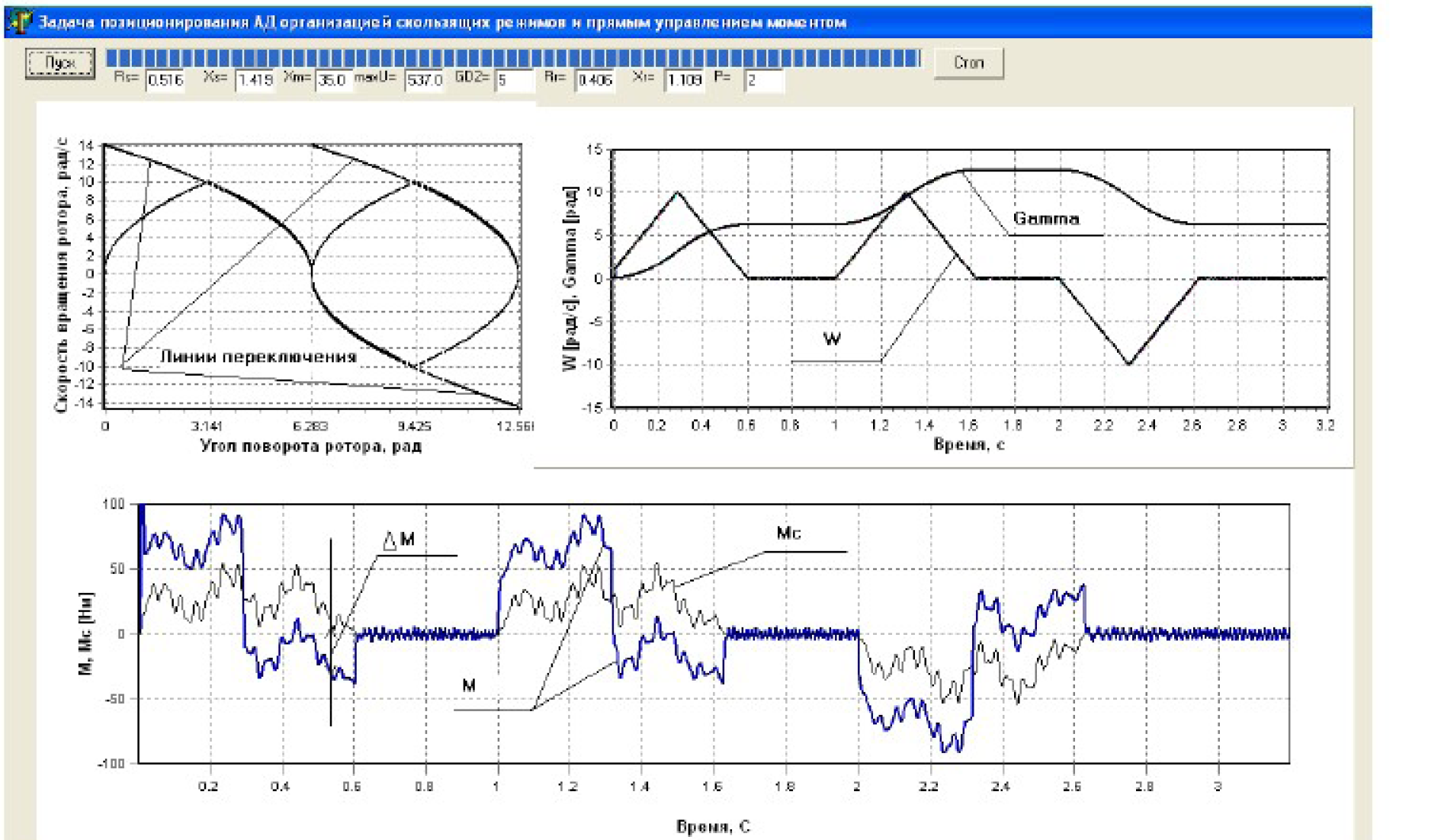
Было разработано программа в среде разработке Delphi, результаты расчетов приведены на рисунке 4:
где
- Указаны паузы.
- Указан поворот ротора АД на угол 2π и 4π.
- Возврат его в положение с углом поворота — 2π при изменении момента сопротивления и обеспечении постоянства динамического момента.
Результатом исследования стало получения следующих результатов:
- Произведен вывод уравнения управления электродвигателем.
- Проверена работоспособность методики в программной среде Matlab Simulink.
- Разработано программное обеспечение в среде Delphi, на основании полученной модели управления.
Список литературы
- Общая задача управления асинхронным электродвигателем/ Ещин Е.К., Григорьев А.В. // ИВУЗ, Электромеханика, 2010 №1. С.39-43.
- Общая задача оптимизации частотного управления асинхронным электродвигателем/ Ещин Е.К., Гаврилов П.Д. // ИВУЗ «Электромеханика». 1979. №6. С.541-545.
- Ковач К.П., Рац И. Переходные процессы в машинах переменного тока М.-Л. Госэнергоиздат, 1963. 744 с.
- Понтрягин Л.С., В.Г. Болтянский, Р.В. Геилкрелидзе, Е.Ф. Мищенко. Математическая теория оптимальных процессов. М Наука, 1983. 392 с.
- YOON-SEOK HAN. The position control of induction motors using a binary disturbance observer / YOON-SEOK HAN.YOUNG-SEOK KIM, SHIGERU OKUMA//AdvancedRobotics, Vol 14,No 2,pp. 119-134 (2000).
- Ещин Е.К., Григорьев А.В., Соколов И.А., Способ управления величиной электромагнитного момента электрической машины переменного тока (варианты). Пат. №2395157 Заявл. 31.03.2008, 0публ. 20.07.2010 Бюл. № 20.
- Utkin V.I., Guldner J., Shi J Sliding mode control in electromechanical systems. Taylor & Francis, 1999 — 325 c.
- Park Min-Но. Chattenng reduction in the position control of induction motor using the sliding mode / Park Min- Ho, Kim Young-Real // Электронный ресурс: http//ieeexplore.ieee.org/xpl/freeabs_all.jsp?amumber=85898.
- Do Thi Hong Them, Durong Hoai Nghia Sliding mode control of induction motor // International Symposium on Electrical & Electronic Engineering 2001 — Oct 24, 25 2007.
- Оптимальное управление координатами асинхронного электродвигателя.
Источник: Управление позиционированием электропривода с асинхронным электродвигателем / Е.К. Ещин // Вестник КузГТУ. — 2012. — №3. — C. 139-141.