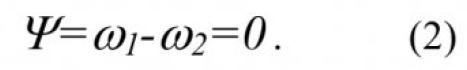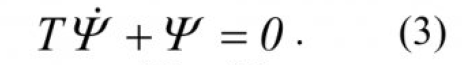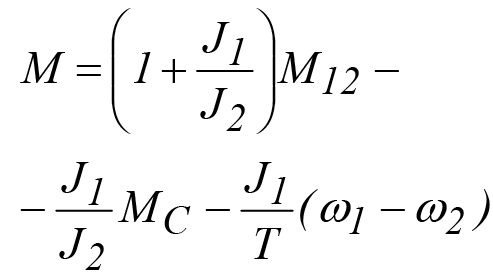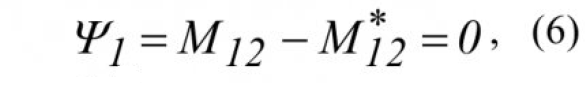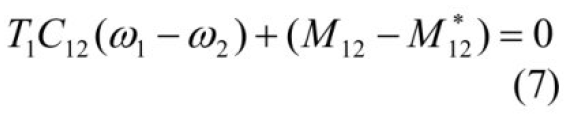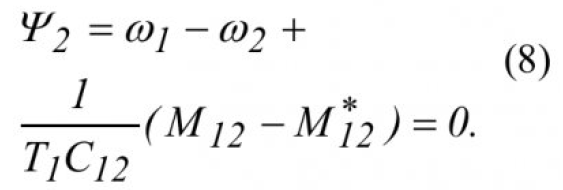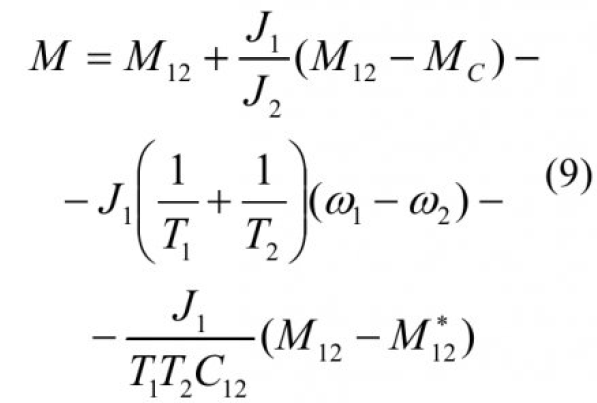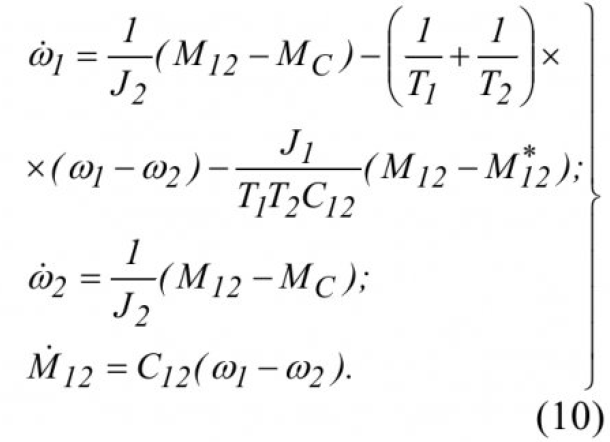Содержание
Существенная доля отказов горных машин связана с выходом из строя элементов трансмиссии.
Одной из основных причин поломки элементов трансмиссии является наличие усталостных явлений, вызванных упругими колебаниями, которые возникают в переходных процессах пуска и останова электропривода, а также под действием нагрузки, которая носит резкопеременный характер.
Вывод математической модели для закона управления
Очевидно, что подавление упругих колебаний в трансмиссиях горных машин является эффективным средством повышения их надежности.
Рассмотрим способ такого подавления для машин, расчетная схема которых представима в виде двухмассовой механической системы с пренебрежением потерь и внутреннего вязкого трения.
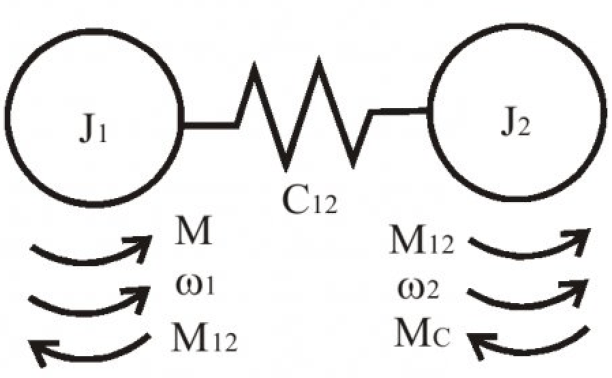
Представим следующую схему двухмассовой механической системы согласно рисунка 1:
Запишем математическую модель данной системы в форме Коши:
где
- М12 — момент упругих сил.
- С12 — коэффициент жесткости упругой связи.
- Мс — момент сопротивления, а именно возмущающее воздействие.
- ω1, ω2, J1, J2 — частоты вращения и моменты инерции первой и второй масс.
- М — момент сил, прикладываемых к системе, а именно управляющее воздействие.
Из третьего уравнения системы (1) видно, что упругие колебания будут отсутствовать в том случае, когда частоты вращения первой и второй масс будут совпадать.
Исходя из этого, в соответствии с синергетической теорией управления согласно работы [1], выберем желаемое инвариантное многообразие следующего вида:
При движении системы вдоль заданного инвариантного многообразия Ψ гарантируется отсутствие упругих колебаний.
Для того чтобы получить управляющее воздействие, гарантирующее выход системы из любой точки фазового пространства на инвариантное многообразие, и дальнейшее движение вдоль него.
Поэтому необходимо решить следующее функциональное уравнение относительно макропеременной Ψ:
Подставив полученное выражение в уравнение (2) в уравнение (3), получаем следующее выражение:
В полученном уравнении избавимся от производных ώ1 и ώ2, заменив их на правые части первого и второго уравнений системы (1):
Учитывая, что управляющим воздействием в системе является подводимый к ней момент сил M, выразим его из уравнения (4).
В результате чего получим закон управления, подавляющий упругие колебания в двухмассовой механической системе:
Компьютерное моделирование и корректировка закона управления
На основании полученной математической модели, произведем компьютерное моделирования полученного закона управления для двухмассовой механической системы.
Для расчетов на ПК примем следующие параметры системы:
- Т=0.01.
- J1=1 кг*м2.
- J2=1 кг*м2.
- С12=1000 Н*м/рад.
Итогом расчетов стало формирование графика трендов представленных на рисунке 2:
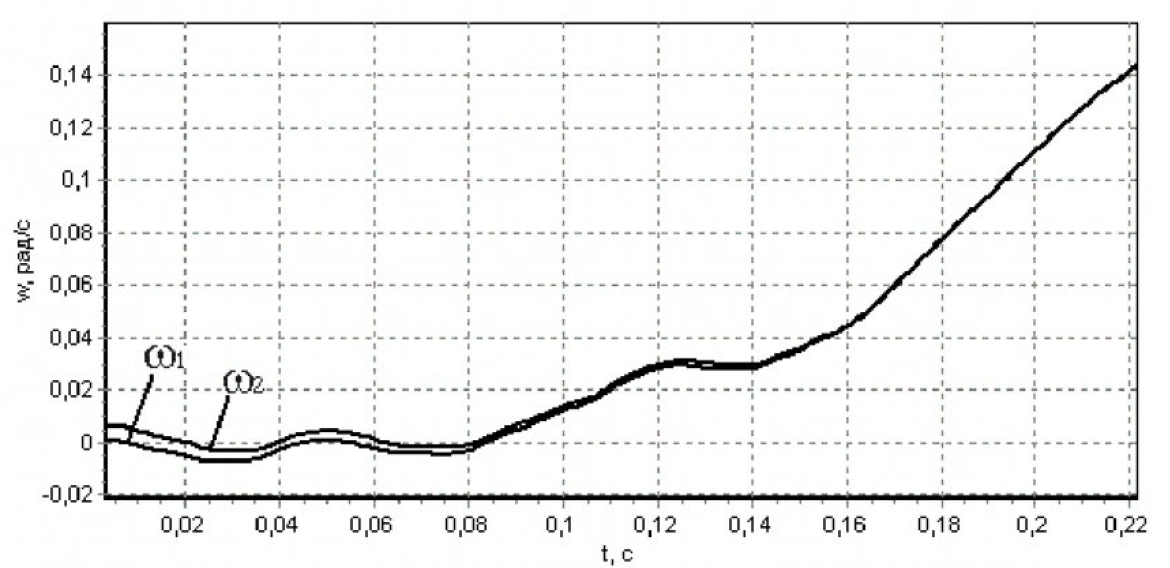
На графиках рисунка 2 можно отследить следующие закономерности:
- Частоты вращения первой и второй масс сходятся в одну линию в течение 0,15 с, что свидетельствует о стабилизации момента упругих сил М12.
- Однако полученный закон управления (5) имеет существенный недостаток, заключающийся в том, что в нем отсутствует какое либо, задающее воздействие.
- Поэтому при помощи данного закона нельзя регулировать ни величину скорости, ни величину момента.
Для исключения данного недостатка осуществим синтез закона управления двухмассовой системой с использованием следующего желаемого инвариантного многообразия:
где
- М*12 — желаемое значение момента упругих сил.
Из полученного уравнения следуют следующие действия:
- Очевидно, что, задав М*12=const, при выходе системы на инвариантное многообразие или по другому сказать, упругие колебания будут подавляться.
- В то же время, изменяя М*12 можно воздействовать на ускорение механической системы, а значит и на ее скорость.
- Решив функциональное уравнение T1Ψ1+Ψ1=0 для инвариантного многообразия (6).
- Далее, подставив правую часть третьего уравнения системы (1) и приняв М*12 =const.
На основании данных преобразований получим:
Из полученного уравнения следует:
- Здесь отсутствует подводимый к двухмассовой механической системе момент сил, являющийся управляющим воздействием.
- Поэтому, в соответствии с концепцией динамического сжатия фазового пространства, известной в теории синергетического управления [1].
- Ведем в систему внутреннее управление, в качестве которого выберем частоту вращения первой массы.
Выберем следующее желаемое инвариантное многообразие для внутреннего управления:
- Ψ=ω1-ʋ=0
где
- ʋ — желаемая траектория движения переменной ω1, полученная из (7).
Следовательно желаемая траектория определяется следующим образом:
Таким образом, получаем следующее инвариантное многообразие, движение по которому гарантирует стабилизацию момента упругих сил M12 на заданном уровне:
Решение функционального уравнения T2Ψ2+Ψ2=0 совместно с уравнением (1) и уравнение (8) дает закон управления:
В итоге получили закон при котором система из любой точки фазового пространства попадет на инвариантное многообразие (6), после чего будет двигаться вдоль него.
С учетом полученного закона управления динамическое поведение замкнутой двухмассовой механической системы будет описываться следующей системой уравнений:
На основании полученной системы уравнений произведем компьютерное моделирование системы.
При моделировании используем следующие параметры системы:
- Т1=0,02.
- T2=0,02.
- J1=1 кг*м2.
- J2=1 кг*м2.
- М*12=15 Н*м.
- С12=1000 Н*м/рад.
При расчетах учтена, резкопеременная составляющая нагрузки моделировалась с использованием фрактального броуновского движения согласно работ [2 и 3].
Результаты компьютерного моделирования работы двухмассовой механической системы с законом управления (10) представлены на рисунке 3:
Из результатов компьютерного моделирования видно:
- Что момент упругих сил достигает заданного значения без перерегулирования за 0,12 с, после чего стабилизируется, несмотря на резкопеременный характер нагрузки.
- В то же время, воздействуя на заданный упругий момент, можно воздействовать на среднюю скорость движения рабочего органа, например, для поддержания оптимальной производительности горной машины.
Таким образом, полученный закон управления упругим моментом может быть рекомендован для использования в системах управления электроприводами горных машин для увеличения их срока службы.
Список литературы
- Современная прикладная теория управления, Синергетический подход в теории управления / Под редакцией А.А. Колесникова — Таганрог: Издательство ТРТГУ, 2000 год, часть II, страница 559.
- Р.М. Кроновер, Фракталы и хаос в динамических системах, Основы теории — Москва: Постмаркет, 2000 год, страница 352.
- Методы классической и современной теории автоматического управления, Том 5, Методы современной теории автоматического управления / Под редакцией К.А. Пупкова — Москва: Издательство МГТУ имени Н.Э. Баумана, 2004 год, страница 287.
- Структура вычислительной части испытательного стенда для оценки параметров и состояния асинхронных электродвигателей.
Источник: Подавление упругих колебаний в горных машинах с двухмассовой расчетной схемой / В.М. Завьялов // Вестник КузГТУ, 2005 год, №6, страницы 67-69.