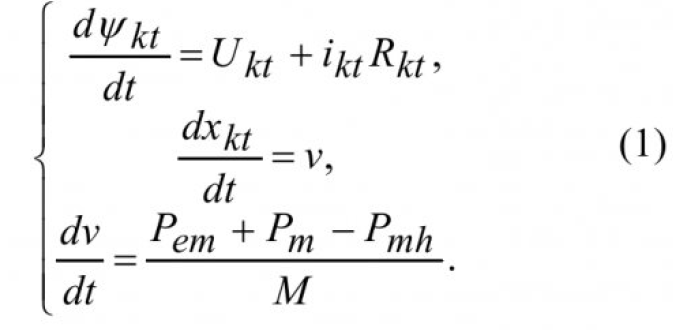Содержание
Известно, что режимы работы и характеристики асинхронного электродвигателя (АД), получающего питание через протяженную кабельную сеть, существенно отличаются от режимов работы и характеристик АД без кабеля.
Наличие кабельной сети особенно сказывается на состоянии АД в режимах, сопровождающихся значительными величинами токов электродвигателя.
Одним из таких режимов является пуск АД.
Значительные величины пусковых токов обеспечивают рост падения напряжения на участке кабельной сети от силового трансформатора до электродвигателя и снижение напряжения на статоре АД со всеми вытекающими отсюда последствиями.
Процессы, происходящие в таких электротехнических комплексах подробно рассмотрены, например, в работах [5 и 6].
Данные комплексы состоят из:
- Кабельной сети.
- Трансформатора.
- Электродвигателей.
Влияние коммутационной аппаратуры на запуск электродвигателя
Вместе с тем следует отметить, что в этих работах не учитывалось возможное реальное влияние коммутационной аппаратуры (пускателей) на АД, в частности:
- Дело в том, что при изменении уровня напряжения на статоре электродвигателя из-за наличия протяженной кабельной сети в определенных режимах работы АД меняется состояние и электродвигателя, и пускателя.
- При питании АД через протяженную кабельную сеть в определенных режимах работы электродвигателя, пускатель и АД становятся взаимозависимыми элементами электротехнического комплекса — трансформатор — кабель — пускатель — электродвигатель.
Это означает необходимость работы по дальнейшему совершенствованию моделей из работ [5 и 6], в части введения в их структуру соответствующих математических моделей коммутационной аппаратуры.
Ниже рассматривается математическая модель электромагнита контактора серии КТУ, получившего широкое распространение в рудничных пускателях.
В частности, рассматривается контактор серии КТУ-4Б, который используется в пускателе ПВИ-250.
Рассматриваемая модель позволяет получить статические и динамические характеристики электромагнита контактора.
Описание конструкции контактора можно найти в источнике [3], а именно:
- Контактор имеет подвижную прямоходную систему, приводимую в движение якорем электромагнита.
- Используемая П-образная магнитная система электромагнита контактора широко используется и в других типах электромагнитов.
- На каждый стержень надет каркас с катушкой.
- Катушки соединяются последовательно и согласно, то есть так, чтобы магнитные потоки в магнитопроводе, создаваемые токами в катушках, были направлены согласно.
П-образная магнитная система контактора КТУ-4Б представлена на рисунке 1:
На рисунке отображены геометрические размеры магнитной системы и состав:
- L — длина стержня сердечника (высота обмотки).
- a, b, с, d — геометрические размеры сердечника.
- 1 — якорь.
- 2 — левый и правый стержень сердечника катушек намагничивания, которые включены последовательно.
Для упрощения расчёта магнитной системы примем:
- Что обмотки намотаны равномерно по всей длине стержней, то есть распределение магнитодвижущей силы — линейно от О, у основания сердечника, до величины равной 2ωI, у воздушного зазора.
- Через рабочие зазоры δ с сопротивлением Rδ проходит рабочий поток Фδ.
- Между стержнями магнитопровода проходит плоскопараллельный поток рассеяния Фδ.
Как видно из принципиальной электрической схемы контактора в момент включения рисунок 2, обмотки питаются выпрямленным двухполупериодным напряжением U=380 B:
Произведём расчет динамических характеристик электромагнита, работающего на постоянном напряжении.
Исходные дифференциальные уравнения электромагнита согласно работе [1]:
где
- М- масса якоря.
- Ukt — напряжение питания.
- v — скорость движения якоря.
- ikt — ток, протекающий по обмотке.
- Rkt — активное сопротивление обмотки.
- Рет — электромагнитная сила притяжения якоря.
- Ψkt — суммарное потокосцепление обмотки электромагнита контактора.
- Pmh — суммарная сила механизма, противодействующая электромагнитной.
- xkr — расстояние между якорем контактора и сердечником магнитной системы (отсчитывается от положения якоря при максимальном зазоре).
- Рт — сила веса якоря, в зависимости от рассматриваемой конструкции контактора, может действовать в ту же сторону, что и электромагнитная сила, или в противоположную ей сторону.
Ток контактора ikt и электромагнитная сила Рет есть функции, зависящие от текущего положения якоря xkt, и текущего потокосцепления Ψkt.
На основе методики расчёта магнитной системы по участкам, описанной в работах [1 и 2], была написана программа расчёта электромагнита в среде Delphi, позволяющая строить как статические, так и динамические характеристики электромагнита.
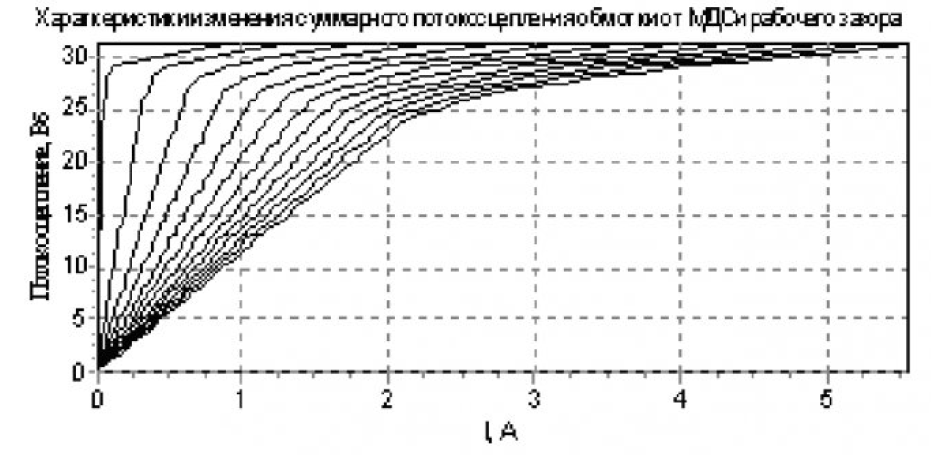
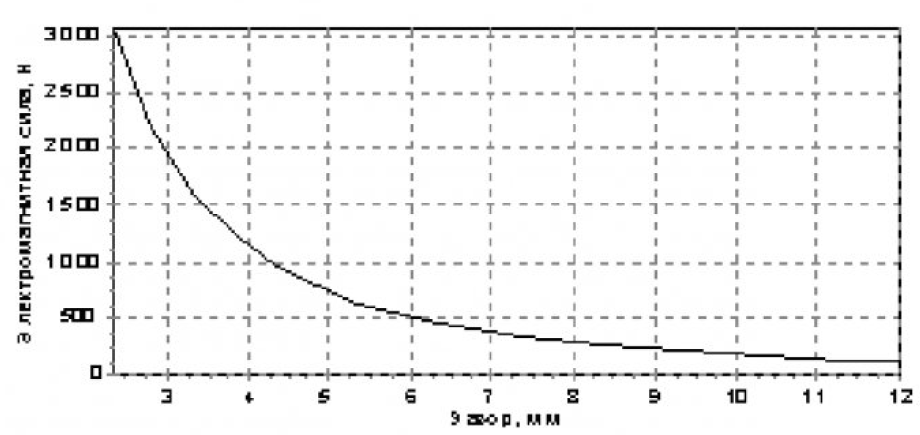
Статические характеристики электромагнита контактора серии КТУ-4Б представлены на рисунках с 3 по 5:
Расчёт магнитной цепи при использовании математического аппарата
Способ расчёта магнитной цепи по участкам вносит определённую погрешность в расчёт, так как изначально допускаются упрощения, которые искажают картину магнитного поля.
Приблизиться к более точным значениям в расчёте магнитной цепи возможно при использовании математического аппарата, основанного на применении метода конечных элементов (МКЭ).
При решении этих задач используется уравнение Пуассона для векторного магнитного потенциала A:
- B=rot(A).
В рассматриваемых задачах вектор индукции В всегда лежит в плоскости модели ху, а вектор плотности стороннего тока j и векторный потенциал А перпендикулярны к ней.
Из программ моделирования магнитных полей МКЭ были рассмотрены:
- Elcut ver/2.2.2.4.
- QuckField ver/ 5.0.3.49.
- комплекс программ ANSYS (R) Release 5.7.1, а в частности ANSYS/Emag 3D.
Анализ софта показал следующее:
- Первые две программы представляют собой очень схожий между собой математический аппарат по двухмерному моделированию МКЭ с тем различием, что QuckField позволяет программного управлять моделью (её свойствами), из других приложений, таких как C++ и VBA, а также имеет встроенный пакет программного управления моделью «Label Mover».
- Одним из существенных недостатков этих программ является их двухмерность и, как следствие этого, невозможность учёта объёмности распределения магнитного поля.
- Программы учитывают объём модели тем, что производят моделирование в третьем измерении на единицу длины, то есть на 1 метр.
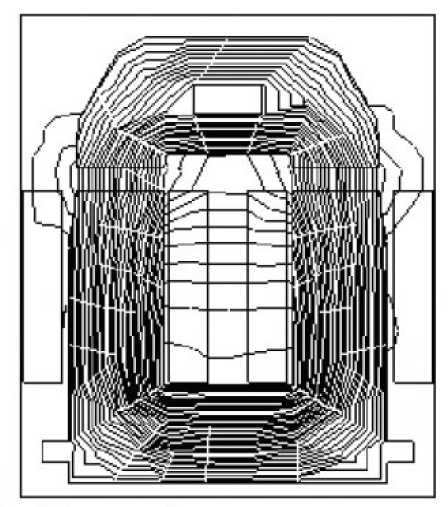
В качестве примера ниже представлен рисунок 6:
где
- Представлен результат решения в пакете ELCUT задачи магнитостатики.
Программа ANSYS/Emag 3D позволяет создавать трёхмерные модели магнитных цепей.
На рисунке 7 показано распределение магнитной индукции по объёму модели:
Проведённый проверочный расчёт тяговой характеристики электромагнита методом конечных элементов, показал:
- Что погрешность, возникающая при расчёте магнитной цепи методом участков, невелика (5-10%).
- При расчёте контактора также была проведена проверка полученных данных с экспериментальными данными работы [4] по тяговой характеристике.
- Расхождение не превышает 5-10%, что приемлемо для расчётов магнитных цепей.
Таким образом, расчёт магнитной цепи можно проводить методом участков.
Расчет динамических характеристик по полученной системе уравнений
Динамические характеристики в работе рассчитывались по системе уравнений (1) методом Рунге-Кутта 4 -го порядка, где учитываются следующие факторы:
- Для того, чтобы контактор мог надёжно замыкать свои главные контакты при снижении напряжении сети при пуске мощного асинхронного двигателя до 0.6 от UH, в момент включения контактора, его электрическое сопротивление равно сопротивлению двух последовательно включённых обмоток Rm=2*257 Ом.
- Данное сопротивление является предельным по плотности тока для данных обмоток — происходит их нагрев, а при длительном режиме работы они выйдут из строя.
- Чтобы этого избежать, после замыкания магнитной системы, в цепь питания обмотки контактора вводится дополнительное сопротивление Rdon=11 кОм, ограничивающее ток обмотки до значений, при которых она может работать в длительном режиме при номинальной температуре.
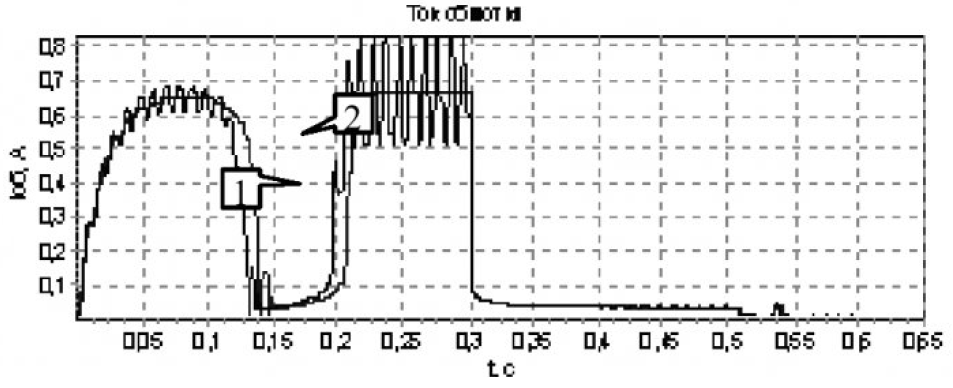
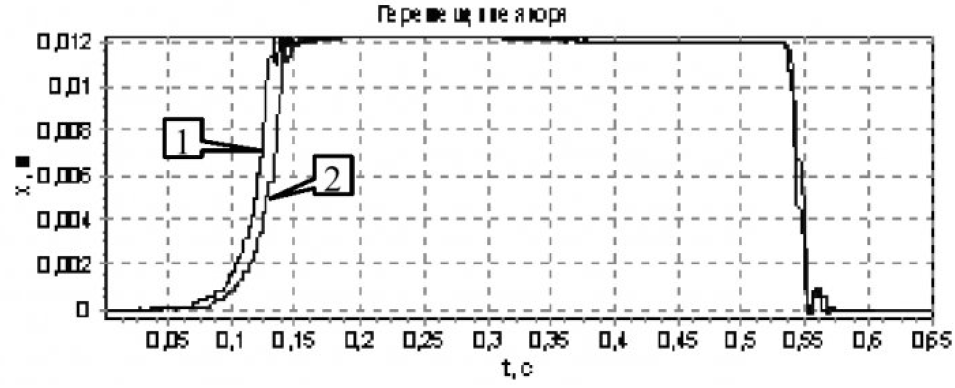
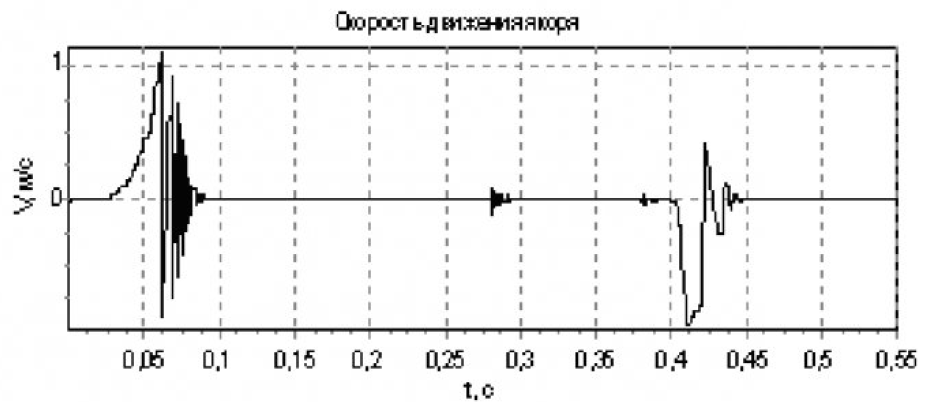
На рисунках с 8 по 11 представлены временные диаграммы работы контактора при введении в цепь обмотки добавочного сопротивления в момент времени t=0.28 с:
Для просмотра динамики отключения, в момент t=0.38 c, введём в цепь обмотки значительное сопротивление, при котором развиваемая электромагнитная сила притяжения якоря будет меньше суммарной противодействующей.
На каждом из рисунках с 8 по 11 представлено по 2 динамические характеристики:
- 1 — показывает работу электромагнита на выпрямленное напряжение 380 В.
- 2 — показывает постоянное напряжение (среднее действующее значение) 342 В.
На основании проведенных изысканий и графиков следует:
- Спад кривой тока (практически до нуля) на участке времени от 0,07 до 0,13 с соответствует значительному росту потокосцепления рисунок 11 в эти моменты времени и, как следствие, росту ЭДС самоиндукции, которое и уменьшает значение тока в обмотке.
- Замыкание магнитной системы происходит в тот момент, когда кривая хода якоря достигает установившегося значения (в данном примере xkt=0,012 м).
- Пульсации кривой перемещения, при достижении установившегося значения, обусловливаются ударом якоря по полюсным наконечникам, происходит «отскок» якоря в начальный момент замыкания П-образной магнитной системы и дальнейшее притяжение якоря к магнитной системе.
- График скорости движения наглядно отображает силы, действующие на якорь в тот или иной момент времени.
- Сравнение полученных динамических характеристик с экспериментальными [4] показывает, что расхождение не превышает 5%.
- Например, согласно работы [4] ток обмотки достигает своего установившегося значения за 0,138 с, по данным этого расчёта за 0,14 с расхождение в 2%.
Таким образом, можно говорить о применимости исследуемой модели для описания электромеханических процессов в электромагните и о возможности ее использования при моделировании последнего в электротехническом комплексе.
Список литературы
- Переходные процессы в электрических машинах и аппаратах и вопросы их проектирования: Учебное пособие для ВУЗов / Гольдберг О.Д., Буль О.Б., Свириденко И.С., Хелемская С.П.; Под редакцией О.Д. Гольдберга -Москва: Высшая школа, 2001 год, иллюстрация со страницы 512.
- Буль О.Б., Компьютерная графика на QwickBasic для электрических аппаратов: Учебное пособие для ВУЗов — Москва: Издательство МГОУ, 1998 год, страница 472, иллюстрация 102.
- Чумаков В.А., Глухов М.С., Осипов Э.Р. и другие, Под редакцией В.В. Дегтярёва, Л.В. Седакова., Руководство по ревизии, наладке и испытанию подземных электроустановок шахт.
- Техническая информация, Разработка и испытание схемы и устройства управления контакторами КТУ-4 при снижении напряжения на их втягивающих катушках до 0.6 Uн. Государственный институт по проектированию и исследованию взрывобезопасного электрооборудования «ГИПРОНИСЭЛЕКТРОШАХТ» 1967 год.
- Ещин Е.К., Моделирование электромеханических процессов многодвигательных электроприводов горных машин — Кемерово: Кузбасский государственный технический университет, 1999 год, страница 115.
- Ещин Е.К., Электромеханические системы много двигательных электроприводов. Моделирование и управление — Кемерово: Кузбасский государственный технический университет, 2003 год, страница 247.
- Модель асинхронного электродвигателя с кабелем и устройством коммутации в статорной цепи.
Источник: Модель электромагнита контактора серии КТУ-4Б / А.В. Губенков // Вестник КузГТУ, 2004 год, №2, страницы 73-76.